6 Гетероскедастичність
6.1 Огляд явища гетероскедастичності
Нагадаю припущення щодо побудови моделей лінійної регресії:
Наша вибірка (\(x_k\) і \(y_i\)) була сформована з генеральної сукупності випадковим чином.
\(y\) — це лінійна функція]* \(\beta_k\) та \(u_i\).
Не має чистої мультиколінеарності у вибірці.
Пояснювальні змінні є екзогенними: \(\mathop{\boldsymbol{E}}\left[ u \middle| X \right] = 0 \left(\implies \mathop{\boldsymbol{E}}\left[ u \right] = 0\right)\)
Залишки мають постійну дисперсію \(\sigma^2\) і нульову коваріація, тобто,
- \(\mathop{\boldsymbol{E}}\left[ u_i^2 \middle| X \right] = \mathop{\text{Var}} \left( u_i \middle| X \right) = \sigma^2 \implies \mathop{\text{Var}} \left( u_i \right) = \sigma^2\)
- \(\mathop{\text{Cov}} \left( u_i, \, u_j \middle| X \right) = \mathop{\boldsymbol{E}}\left[ u_i u_j \middle| X \right] = 0\) для \(i\neq j\)
- Залишки мають нормальний розподіл, тобто \(u_i \overset{\text{iid}}{\sim} \mathop{\text{N}}\left( 0, \sigma^2 \right)\) (iid, independent and identically distributed, незалежні та однаково розподілені).
У цьому розділі ми сконцентруємо свою увагу на п’ятому припущенні щодо постійності дисперсії, яка називається гомоскедастичністю.
Якщо дисперсія залишків непостійна — таке явище називається гетероскедастичснітю: \(\mathop{\text{Var}} \left( u_i \right) = \sigma^2_i\) та \(\sigma^2_i \neq \sigma^2_j\) для деяких \(i\neq j\)
Класична гетероскедастичність залишків виглядає так: дисперсія \(u\) збільшується зі збільшенням \(x\)
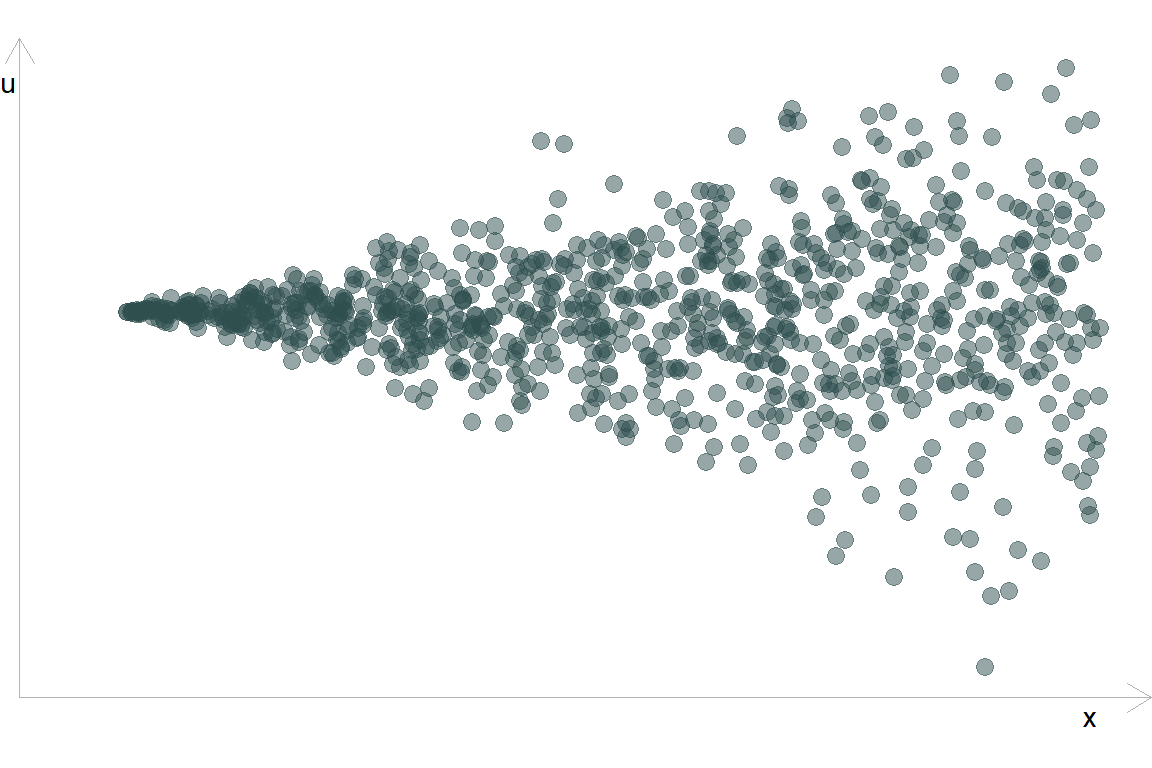
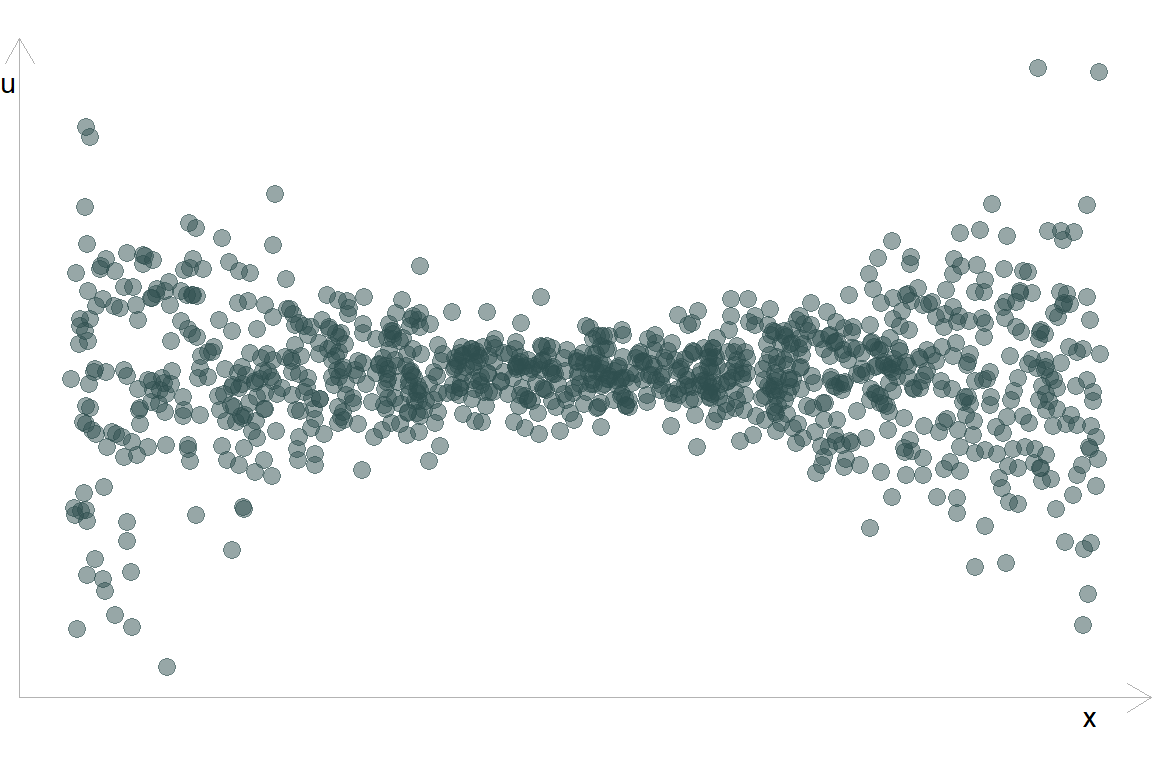
Інший випадок гетероскедастичності: дисперсія \(u\) збільшується за краях \(x\)
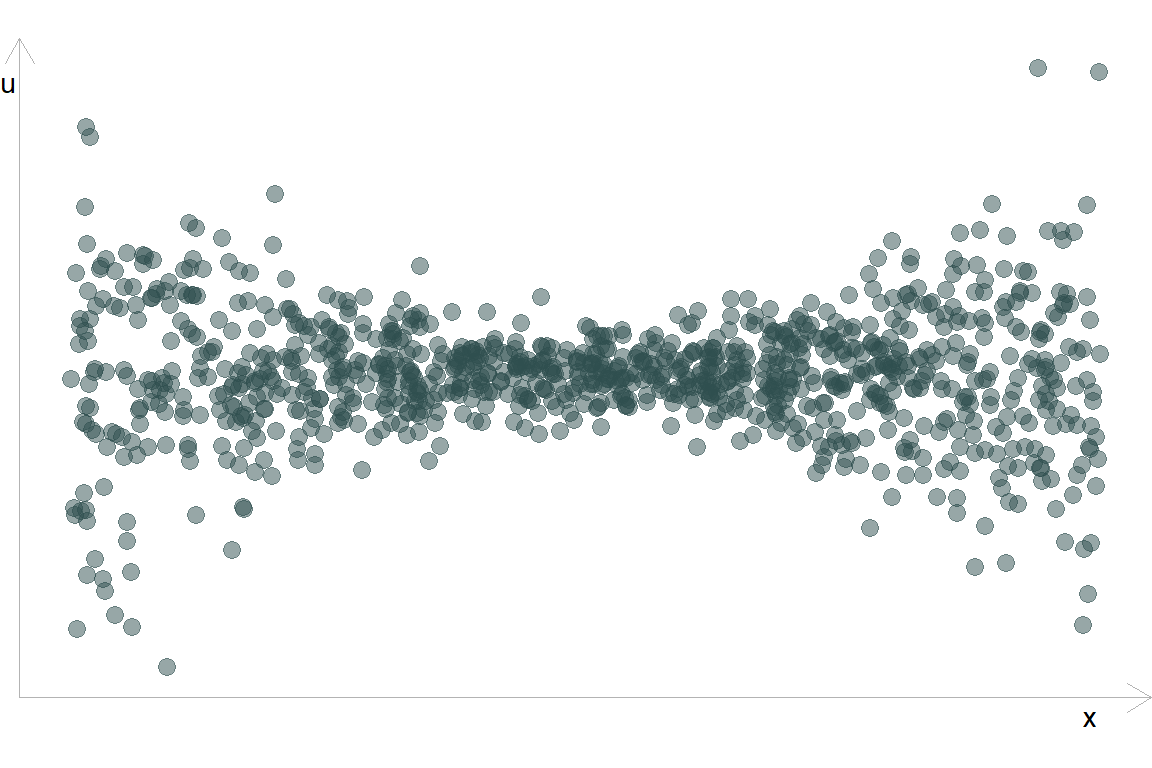
Або так: різна дисперсія \(u\) в різних групах:
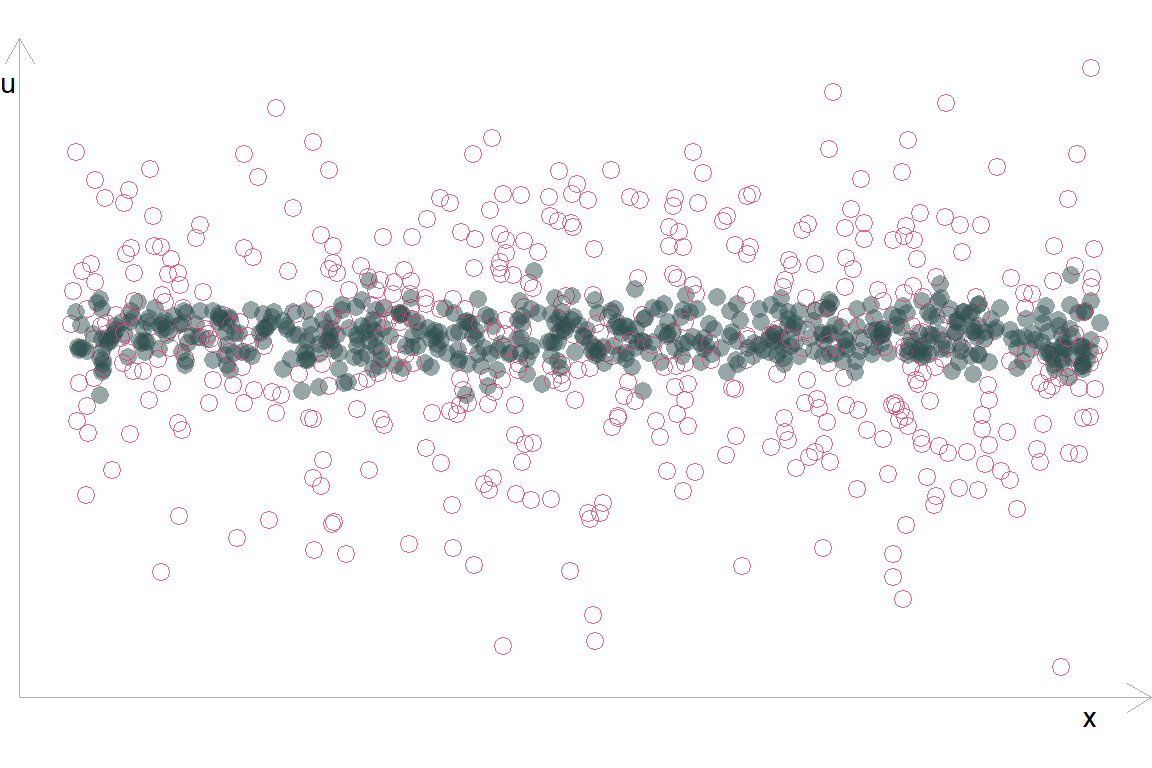
Гетероскедастичність присутня, коли дисперсія \(u\) змінюється за будь-якої комбінацієї пояснювальних змінних від \(x_1\) до \(x_k\) (далі: \(X\)).
Це дуже розповсюджене явище на практиці. Наявність цього явища в моделі негативно впливає на якість МНК моделі.
Основні наслідки гетероскедастичності:
МНК-оцінки залишаються незміщенними.
Ефективність: МНК більше не є найкращім незміщеним варіантом оцінювання моделі.
Статистичний вивід: стандартні похибки оцінок параметрів моделі є зміщенними, що в результаті призводить до хибних довірчих інтервалів та проблем з тестуванням гіпотез (\(t\) та \(F\) тести).
Рішення:
Проводити тестування на наявність гетероскедастичності.
Використовувати підходи до нівелювання наслідків гетероскедастичності.
6.2 Тестування гетероскедастичності
Ефективність наших оцінок залежить від наявності або відсутності гетероскедастичності. Для виявленя цього явища використовуються наступні підходи:
Тест Гольдфельда-Квандта
Тест Брейша-Пагана
Тест Уайта
Кожен з цих тестів зосереджується на використанні залишків МНК \(e_i\) для оцінювання порушенm в \(u_i\).
6.2.1 Тест Гольдфельда-Квандта
Тест G-Q був одним з перших тестів гетероскедастичності (1965). В кьому зосереджено увагу на конкретному типі гетероскедастичності: чи відрізняється дисперсія \(u_i\) між двома групами.
Раніше ми використовували залишки для оцінювання \(\sigma^2\):
\[ s^2 = \dfrac{\text{RSS}}{n-1} = \dfrac{\sum_i e_i^2}{n-1} \]
Ми будемо використовувати цю ж ідею, щоб визначити, чи відрізняється дисперсія в двох групах, порівнюючи \(s^2_1\) і \(s^2_2\).
Алгоритм виконання тесту G-Q:
Впорядкуємо спостереження за \(x\) (який вважаємо призводить до гетероскедастичності)
-
Розділяємо дані на дві групи розміру \(n^*\)
- \(G_1\): перша третина
- \(G_2\): остання третина
Будуємо окремі регресії \(y\) на \(x\) для G1 та G2
Запишіть \(RSS_1\) і \(RSS_2\)
Розраховуємо статистику тесту G-Q:
\[ F_{\left(n^{\star}-k,\, n^{\star}-k\right)} = \dfrac{\text{RSS}_2/(n^\star-k)}{\text{RSS}_1/(n^\star-k)} = \dfrac{\text{RSS}_2}{\text{RSS}_1} \] Голдфельд і Квандт запропонували \(n^{\star}\) із \((3/8)n\). \(k\) кількість розрахункових параметрів (тобто \(\hat{\beta}_j\)).
Статистика G-Q тесту відповідає відповідає розподілу \(F\) зі ступенями свободи \(n^{\star}-k\) і \(n^{\star}-k\).
Зауваження:
- Тест G-Q вимагає, щоб випадкова складова відповідає нормальному розподілу.
- G-Q передбачає дуже специфічний тип/форму гетероскедастичності.
- Дуже добре працює, якщо ми знаємо форму гетероскедастичності.
6.2.1.1 Візуальний приклад
- Припустимо, що ми побудували модель та отримали наступний розподіл залишків відносно впорядкованої змінної \(x\):
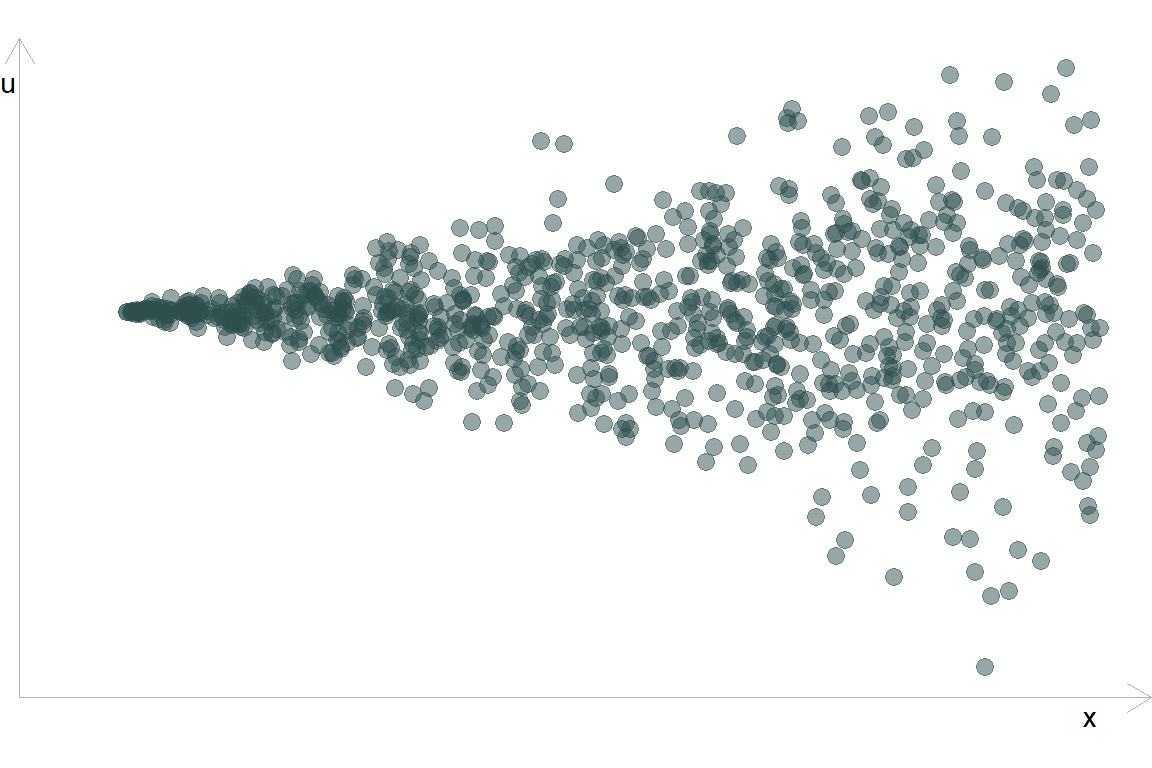
- Поділимо спостереження на групи:
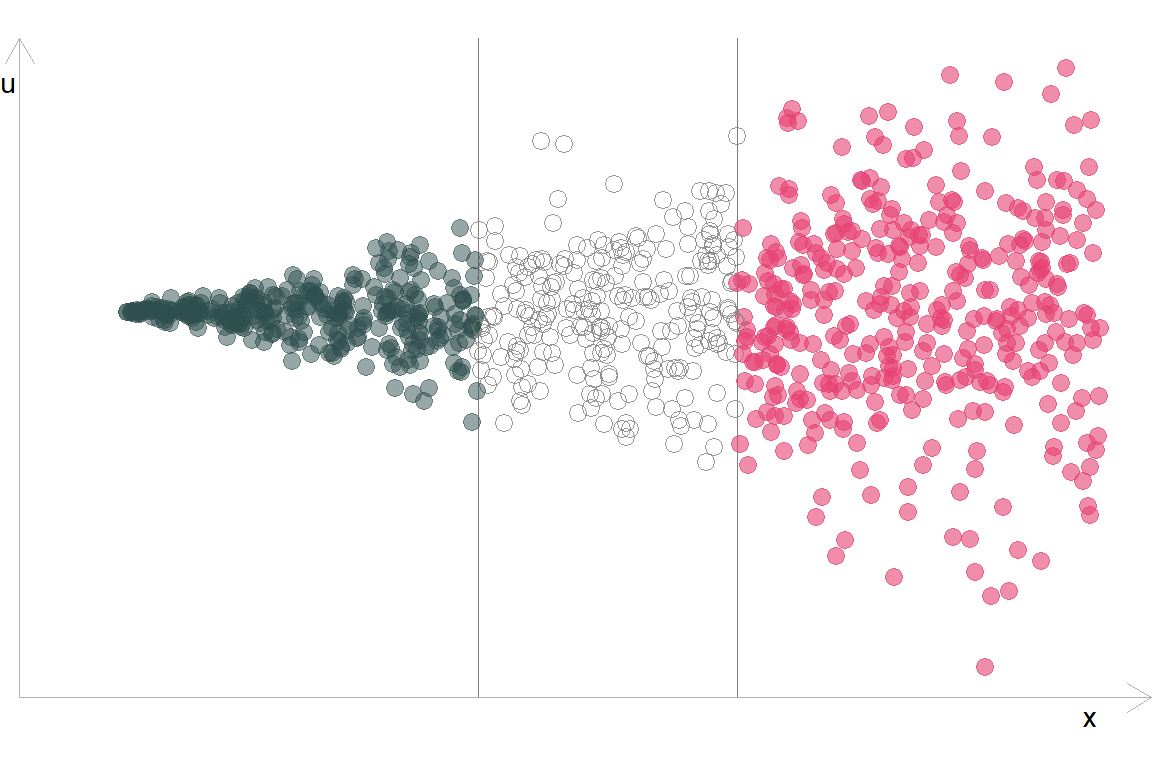
- Розрахуємо статистику
\(F_{375,\,375} = \dfrac{\color{#e64173}{\text{RSS}_2 = 18,203.4}}{\color{#314f4f}{\text{RSS}_1 = 1,039.5}} \approx 17.5 \implies\) p-value \(< 0.001\)
В такому випадку ми відхиляємо \(H_0\): \(\sigma^2_1 = \sigma^2_2\) і робимо висновок, що є статистично значущі докази гетероскедастичності.
6.2.1.2 Недолік тесту
Але в такого підходу є недолік. Якщо наші похибки будуть симетрично змінюватись відносно центру, тест буде приймати нульову гіпотезу:
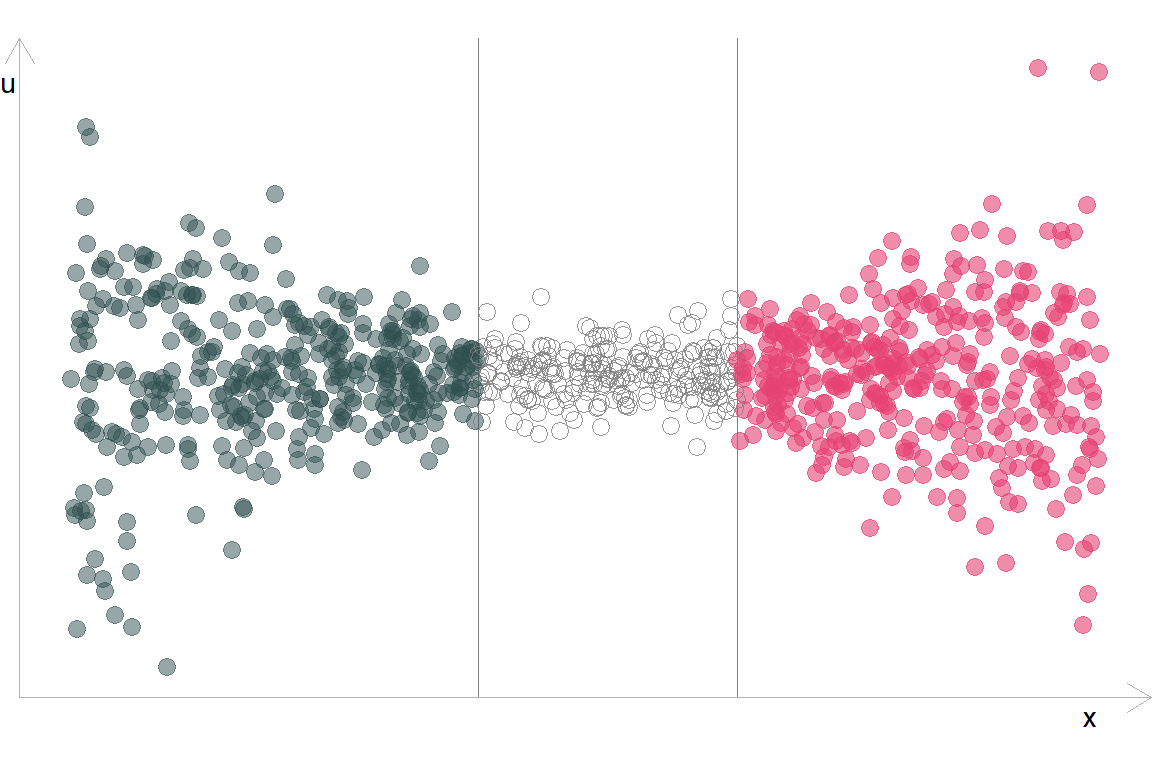
\(F_{375,\,375} = \dfrac{\color{#e64173}{\text{RSS}_2 = 14,516.8}}{\color{#314f4f}{\text{RSS}_1 = 14,937.1}} \approx 1 \implies\) p-value \(\approx 0.609\)
В такому випадку ми не можемо відхилити \(H_0\): \(\sigma^2_1 = \sigma^2_2\) при цьому гетероскедастичність присутня.
6.3 Тест Брейша-Пагана
Breusch і Pagan (1981) намагалися вирішити проблему гетероскедастичності за допомогою функціональної форми:
Будуємо регресію \(y\) від \(X = [1, x_1, x_2, \dots, x_k]\).
Визначаємо залишки моделі \(e\).
Будуємо регресію \(e^2\) від \(X = [1, x_1, x_2, \dots, x_k]\)
\[e_i^2 = \alpha_0 + \alpha_1 x_{1i} + \alpha_2 x_{2i} + \dots + \alpha_k x_{ki} + v_i\].
Визначаємо коефіцієнт детермінації \(R^2\).
Тестуємо статистичну значущість оцінок параметрів моделі, \(H_0: \alpha_1 = \alpha_2 = \cdots = \alpha_k = 0\)
Розрахунок статистики Брейша-Пагана виконується за формулою:
\[LM = n \times R_e^2\]
де \(R_e^2\) коефіцієнт детермінації з моделі регресії \(e_i^2 = \alpha_0 + \alpha_1 x_{1i} + \alpha_2 x_{2i} + \dots + \alpha_k x_{ki} + v_i\)
LM-статистика асимптотично розподілена \(\chi^2_k\).
Відхилення нульової гіпотези передбачає наявність гетероскедастичності.
\(\chi^2_k\) розподіл при \(\color{#314f4f}{k = 1}\), \(\color{#e64173}{k = 2}\), та \(\color{orange}{k = 9}\) має вигляд:
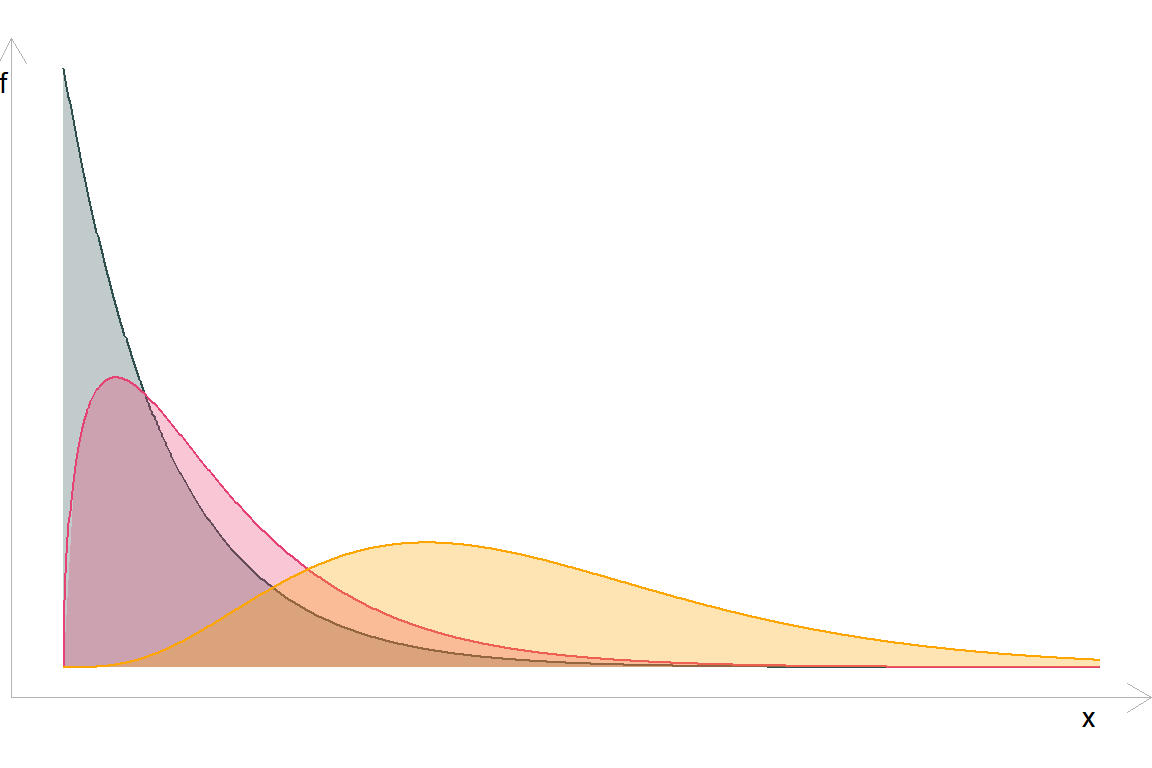
Імовірність спостереження більш екстремальної тестової статистики \(\widehat{\text{LM}}\) під \(H_0\):
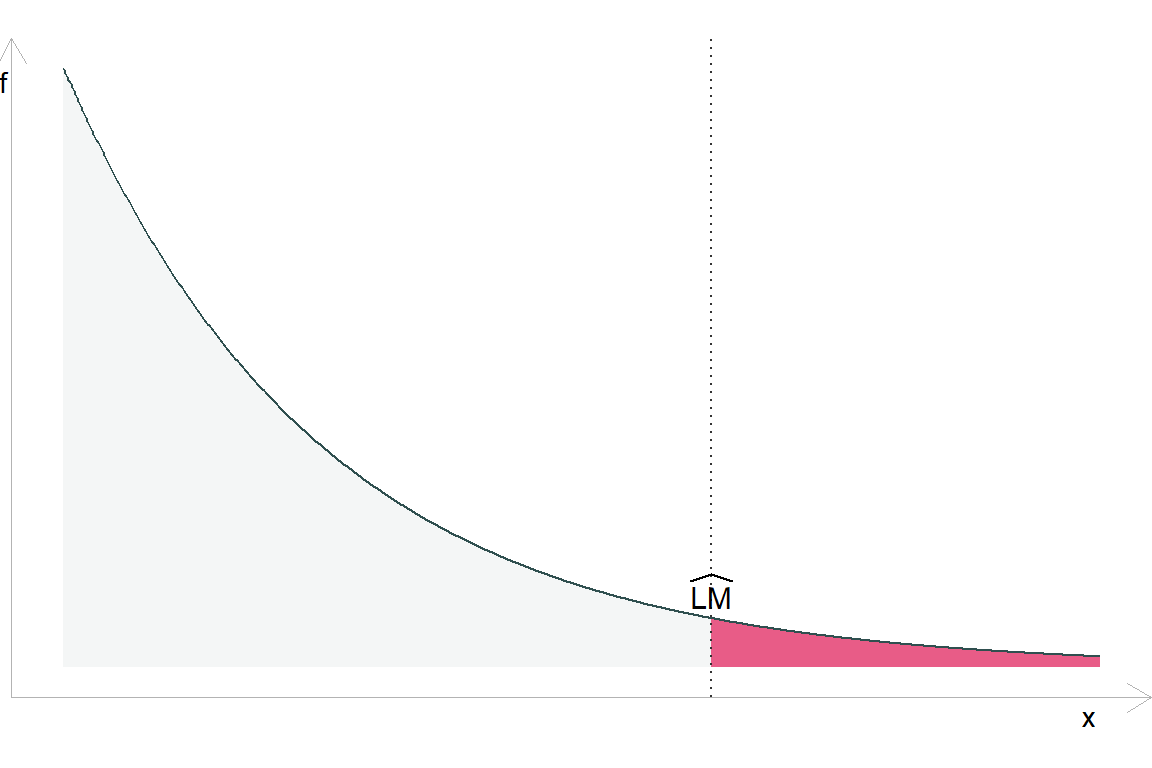
У даного підходу є певний нюанс: ми припускаємо досить простий взаємозв’язок між нашими пояснювальними змінними \(X\) і дисперсією \(\sigma^2_i\). І як результат B-P все ще може упускати прості форми гетероскедастичності.
Тест Брейша-Пагана все ще чутливі до функціональної форми залежності.
\[ \begin{aligned} e_i^2 &= \hat{\alpha}_0 + \hat{\alpha}_1 x_{1i} & \widehat{\text{LM}} &= 1.26 &\mathit{p}\text{-value} \approx 0.261 \\ e_i^2 &= \hat{\alpha}_0 + \hat{\alpha}_1 x_{1i} \color{#e64173}{+ \hat{\alpha}_2 x^2_{1i}} & \widehat{\text{LM}} &= 185.8 &\mathit{p}\text{-value} < 0.001 \end{aligned} \]
6.4 Тест Уайта
До цього ми перевіряли специфічні зв’язки між нашими пояснювальними змінними та дисперсіями разилишків, наприклад,
\(H_0: \sigma_1^2 = \sigma_2^2\) для двох групn \(x_j\) (G-Q)
\(H_0: \alpha_1 = \cdots = \alpha_k = 0\) для \(e_i^2 = \alpha_0 + \alpha_1 x_{1i} + \cdots + \alpha_k x_{ki} + v_i\) (B-P)
Проте ми насправді хочемо знати, чи
\[ \sigma_1^2 = \sigma_2^2 = \cdots = \sigma_n^2 \]
Чи не можна просто перевірити цю гіпотезу? Частково…
Для досягнення цієї мети Хел Уайт скористався тим фактом, що ми можемо замінити вимогу гомоскедастичності більш слабким припущенням:
Раніше: \(\mathop{\text{Var}} \left( u_i \middle| X \right) = \sigma^2\)
Зараз: \(u^2\) не корелює з пояснювальними змінними (тобто, \(x_j\) для всіх \(j\)), їх квадратами (тобто, \(x_j^2\)), і взаємодіями першого ступеня (тобто, \(x_j x_h\)).
Це нове припущення легше перевірити явно (підказка: регресія).
Алгоритм тесту Уайта:
Будуємо регресію \(y\) від \(X = [1, x_1, x_2, \dots, x_k]\). Записуємо залишки \(e\).
Будуємо регресію квадрату залишків до всіх пояснюючих змінних, їх квадратів та взаємодії, тобто
\[ e^2 = \alpha_0 + \sum_{h=1}^k \alpha_h x_h + \sum_{j=1}^k \alpha_{k+j} x_j^2 + \sum_{\ell = 1}^{k-1} \sum_{m = \ell + 1}^k \alpha_{\ell,m} x_\ell x_m + v_i \]
Визначаємо коефіцієнт детермінації \(R_e^2\).
Розраховуємо статистику для перевірки гіпотез \(H_0: \alpha_p = 0\) для всіх \(p\neq0\).
Як і увипадку B-P тесту, статистика тесту Уайта:
\[\text{LM} = n \times R_e^2 \qquad \text{H}_0,\, \text{LM} \overset{\text{d}}{\sim} \chi_k^2\]
але тепер \(R^2_e\) походить від регресії \(e^2\) щодо пояснювальних змінних, їх квадратів та їх взаємодії.
\[ e^2 = \alpha_0 + \underbrace{\sum_{h=1}^k \alpha_h x_h}_{\text{Поясн. змінні}} + \underbrace{\sum_{j=1}^k \alpha_{k+j} x_j^2}_{\text{Квадратна форма}} + \underbrace{\sum_{\ell = 1}^{k-1} \sum_{m = \ell + 1}^k \alpha_{\ell,m} x_\ell x_m}_{\text{Взаємодії}} + v_i \]
Примітка: \(k\) (для нашого \(\chi_k^2\)) дорівнює кількості оцінених параметрів у наведеній вище регресії (\(\alpha_j\)), за винятком \(\alpha_0\).
Практична примітка. Якщо змінна дорівнює її квадрату (наприклад, бінарні змінні), ви не можете включати її. Те саме правило стосується взаємодій.
Приклад: Розглянемо модель \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + u\)
Крок 1: Оцініть модель; отримати залишки \((e)\).
Крок 2: Регресія \(e^2\) щодо пояснювальних змінних, квадратів і взаємодій.
\[ \begin{aligned} e^2 = &\alpha_0 + \alpha_1 x_1 + \alpha_2 x_2 + \alpha_3 x_3 + \alpha_4 x_1^2 + \alpha_5 x_2^2 + \alpha_6 x_3^2 \\ &+ \alpha_7 x_1 x_2 + \alpha_8 x_1 x_3 + \alpha_9 x_2 x_3 + v \end{aligned} \]
Запишіть \(R^2\) з цього рівняння (назвемо його \(R_e^2\)).
Крок 3: Перевірте \(H_0: \alpha_1 = \alpha_2 = \cdots = \alpha_9 = 0\) за допомогою \(\text{LM} = n R^2_e \overset{\text{d} }{\sim} \chi_9^2\).
6.5 Приклади проведення тестів
library(tidyverse)
library(broom)
library(Ecdat)
test_tbl <- Caschool %>%
select(test_score = testscr, ratio = str, income = avginc) %>%
as_tibble()
head(test_tbl, 2)
## # A tibble: 2 x 3
## test_score ratio income
## <dbl> <dbl> <dbl>
## 1 691. 17.9 22.7
## 2 661. 21.5 9.82\[ \left(\text{Test score}\right)_i = \beta_0 + \beta_1 \text{Ratio}_{i} + \beta_2 \text{Income}_{i} + u_i \]
est_model <- lm(test_score ~ ratio + income, data = test_tbl)
tidy(est_model)
## # A tibble: 3 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 639. 7.45 85.7 5.70e-267
## 2 ratio -0.649 0.354 -1.83 6.79e- 2
## 3 income 1.84 0.0928 19.8 4.38e- 62Візуалізація залишків
test_tbl$e <- residuals(est_model)6.5.1 Goldfeld-Quandt
test_tbl <- arrange(test_tbl, income)
est_model1 <- lm(test_score ~ ratio + income, data = head(test_tbl, 158))
est_model2 <- lm(test_score ~ ratio + income, data = tail(test_tbl, 158))
e_model1 <- residuals(est_model1)
e_model2 <- residuals(est_model2)
(sse_model1 <- sum(e_model1^2))
## [1] 29537.83
(sse_model2 <- sum(e_model2^2))
## [1] 19305.01
(f_gq <- sse_model2/sse_model1)
## [1] 0.6535688
pf(q = f_gq, df1 = 158-3, df2 = 158-3, lower.tail = F)
## [1] 0.9957733Висновок:
\(F \approx 0.65\)
p-value \(\approx 0.99577\)
Не відхиляємо нульову гіпотезу.
Розрахуємо за допомогою готових функцій:
library(lmtest)
gqtest(arr_est_model, data = test_tbl, fraction = 104)
##
## Goldfeld-Quandt test
##
## data: arr_est_model
## GQ = 0.65007, df1 = 155, df2 = 155, p-value = 0.9962
## alternative hypothesis: variance increases from segment 1 to 2Результати збігаються!