3 Проста лінійна регресія

Економетрика - це дисципліна, яка займається дослідженням взаємозв’язків між даними. Для цього нам знадобиться знання статистики, математики, економіки. Це може допомогти вирішити дві головні задачі дослідження:

• пояснити зв’язки: визначити які показники впливають сильніше на певні процеси, а які менше.

• будувати прогнози: як буде розвиватися процес в подальшому або при інших умовах.

Уявіть, що вам необхідно оцінити ефективність витрат рекламної компанії, тенденцію розвитку витрат виробництва, прогноз валового внутрішнього продукту тощо. На кожне з цих завдань може допомогти знайти відповідь економетрика, хоча з точки зору прогнозної сили, напевно, слід піти далі і звернутися до алгоритмів машинного навчання або нейронних мереж, хоча й там є свої особливості. На мою думку, економетрика на рівні зі статистикою - це чудовий фундамент для подальшого вивчення машинного навчання.

Для економетричного дослідження необхідно будувати математичні моделі - спрощений варіант реальних об’єктів дослідження. Виглядають вони частіше за все, як певні рівняння, наприклад опишемо залежність заробітної плати робітника від його освіти, досвіду роботи та навичок. Таку залежність можна описати наступним чином:

\[ y = f(x_1, x_2, x_3, \dots, x_n), \tag{3.1} \] де \(y\) — заробітна плата, \(x_1\) — рівень освіти, \(x_2\) — досвід роботи, \(x_3\) — навички (знання мов програмування, статистики тощо), \(x_n\) — інші показники, \(f\) — функція залежності: описує яким саме чином \(x_i\) впливають на \(y\).

Змінна \(y\), яку ми намагаємось пояснити, називається залежною, а змінні \(x_i\), за допомогою яких ми намагаємось пояснити або спрогнозувати залежну змінну, називають незалежними. Хоча можуть зустрічатися і альтернативні визначення:

Y	X
Залежна змінна	Незалежна змінна
Пояснювана змінна	Пояснювальна змінна
Відгук	Контрольна змінна
Прогнозована змінна	Предиктор
Регресант	Регресор
	Коваріат

Зверніть увагу, що ми суб’єктивно оголосили, що на заробітну плату впливають зазначені показники. При альтернативних дослідженні і форма залежності, і перелік змінних може бути іншим. Та й взагалі, можливо ми захочемо пояснити вже рівень освіти за допомогою заробітної плати, досвіду роботи і навичок. Все це ми визначаємо на основі своїх знань, досвіду та доступної інформації.

В якості джерел даних можуть виступати:

• Перехресні дані: дані зібрані по різним об’єктам дослідження (персонал, компанії, держави, сфери тощо). Часто такі дані були зібрані за допомогою простої випадкової вибірки.

library(tidyverse)
starwars
## # A tibble: 87 x 14
##    name  height  mass hair_color skin_color eye_color birth_year sex   gender homeworld
##    <chr>  <int> <dbl> <chr>      <chr>      <chr>          <dbl> <chr> <chr>  <chr>    
##  1 Luke~    172    77 blond      fair       blue            19   male  mascu~ Tatooine 
##  2 C-3PO    167    75 <NA>       gold       yellow         112   none  mascu~ Tatooine 
##  3 R2-D2     96    32 <NA>       white, bl~ red             33   none  mascu~ Naboo    
##  4 Dart~    202   136 none       white      yellow          41.9 male  mascu~ Tatooine 
##  5 Leia~    150    49 brown      light      brown           19   fema~ femin~ Alderaan 
##  6 Owen~    178   120 brown, gr~ light      blue            52   male  mascu~ Tatooine 
##  7 Beru~    165    75 brown      light      blue            47   fema~ femin~ Tatooine 
##  8 R5-D4     97    32 <NA>       white, red red             NA   none  mascu~ Tatooine 
##  9 Bigg~    183    84 black      light      brown           24   male  mascu~ Tatooine 
## 10 Obi-~    182    77 auburn, w~ fair       blue-gray       57   male  mascu~ Stewjon  
## # ... with 77 more rows, and 4 more variables: species <chr>, films <list>,
## #   vehicles <list>, starships <list>

• Часові ряди: дані по одному чи декількох об’єктах дослідження впродовж певного періоду часу (курси валют, ВВП, пасажиропотік тощо). Головною особливістю таких даних виступає часова впорядкованість (від минулого до сучасного) та частота даних (однаковий інтервал запису даних).

economics
## # A tibble: 574 x 6
##    date         pce    pop psavert uempmed unemploy
##    <date>     <dbl>  <dbl>   <dbl>   <dbl>    <dbl>
##  1 1967-07-01  507. 198712    12.6     4.5     2944
##  2 1967-08-01  510. 198911    12.6     4.7     2945
##  3 1967-09-01  516. 199113    11.9     4.6     2958
##  4 1967-10-01  512. 199311    12.9     4.9     3143
##  5 1967-11-01  517. 199498    12.8     4.7     3066
##  6 1967-12-01  525. 199657    11.8     4.8     3018
##  7 1968-01-01  531. 199808    11.7     5.1     2878
##  8 1968-02-01  534. 199920    12.3     4.5     3001
##  9 1968-03-01  544. 200056    11.7     4.1     2877
## 10 1968-04-01  544  200208    12.3     4.6     2709
## # ... with 564 more rows

• Панельні дані: поєднуть в собі перехресні дані та часові ряди, вони показують, як об’єкти дослідження змінювались з часом.

library(gapminder)
gapminder
## # A tibble: 1,704 x 6
##    country     continent  year lifeExp      pop gdpPercap
##    <fct>       <fct>     <int>   <dbl>    <int>     <dbl>
##  1 Afghanistan Asia       1952    28.8  8425333      779.
##  2 Afghanistan Asia       1957    30.3  9240934      821.
##  3 Afghanistan Asia       1962    32.0 10267083      853.
##  4 Afghanistan Asia       1967    34.0 11537966      836.
##  5 Afghanistan Asia       1972    36.1 13079460      740.
##  6 Afghanistan Asia       1977    38.4 14880372      786.
##  7 Afghanistan Asia       1982    39.9 12881816      978.
##  8 Afghanistan Asia       1987    40.8 13867957      852.
##  9 Afghanistan Asia       1992    41.7 16317921      649.
## 10 Afghanistan Asia       1997    41.8 22227415      635.
## # ... with 1,694 more rows

Функція залежності (\(f\)) може мати різну форму та характер. Ми не знаємо її заздалегідь і намагаємось підібрати найкращий варіант з декількох альтернатив.

3.1 Проста лінійна регресія

Проста лінійна регресія — це модель, яка пояснює залежність між двома змінними за допомогою лінійного взаємозв’язку.

Роботу такої регресії краще пояснити на прикладі. В нашому розпорядженні є набір даних про вагу та зріст вибірки чоловіків та жінок:

weight_height <- read_csv("https://raw.githubusercontent.com/Aranaur/datasets/main/datasets/weight-height.csv")

weight_height
## # A tibble: 10,000 x 3
##    Gender Height Weight
##    <chr>   <dbl>  <dbl>
##  1 Male     73.8   242.
##  2 Male     68.8   162.
##  3 Male     74.1   213.
##  4 Male     71.7   220.
##  5 Male     69.9   206.
##  6 Male     67.3   152.
##  7 Male     68.8   184.
##  8 Male     68.3   168.
##  9 Male     67.0   176.
## 10 Male     63.5   156.
## # ... with 9,990 more rows

Конвертуємо значення в кілограми і сантиметри та візуалізуємо підвибірку по чоловікам:

# фіксуємо генератор випадкових величин
set.seed(2022)

male <- weight_height %>% 
  # беремо тільки чоловіків
  filter(Gender == "Male") %>%
  # формуємо випадкову підвибірку
  slice_sample(n = 100) %>% 
  # конвертуємо значення
  mutate(Height_kg = Height * 2.54,
         Weight_cm = Weight * 0.45)

# візуалізуємо
male %>% 
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  labs(x = "Зріст (см)",
       y = "Вага (кг)")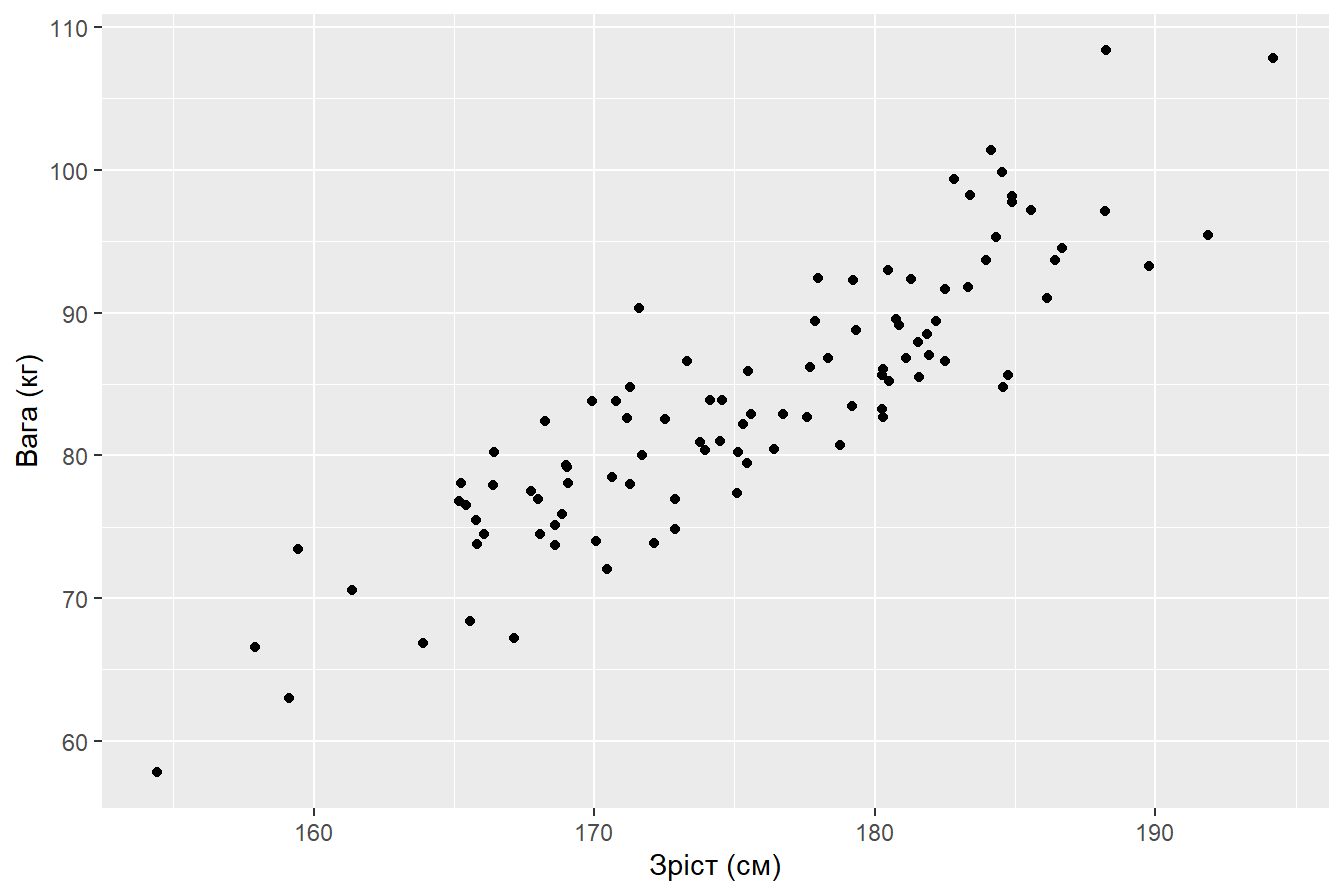

Припустимо, що взаємозв’язок між вагою і зростом - лінійний. Такі випадки на практиці досить рідко зустрічаються і пізніше ми познайомимось з іншими варіантами.

Рівняння прямої виглядає наступним чином: \[ y_i = \beta_0 + \beta_1x_i + u_i \tag{3.2} \] Підставимо конкретні змінні у рівняння, отримаємо: \[ Weight_i = \beta_0 + \beta_1Height_i + u_i \tag{3.3} \] Рівняння (3.2) та (3.3) називаються простою лінійною регресією або парною лінійною регресією.

Розглянемо складові рівняння (3.2):

• \(y\): залежна змінна.

• \(\beta_0\): вільний параметр моделі, який відповідає за точку перетину прямої з вістю ординат.

• \(\beta_1\): залежний параметр моделі, який відповідає за кут нахилу прямої.

• \(x\): незалежна змінна.

• \(u\): залишки моделі.

Для того щоб тримати рівняння прямої, нам необхідно підібрати значення параметрів моделі: \(\hat{\beta_0}\) та \(\hat{\beta_1}\). Що значать “кришки” \(^\) над коєфіціентами? Справа в тому, що в нашому розпорядженні є тільки певна вибірка даних і провести ідеальну пряму через всі точки неможливо. Тому нам необхідно розрахувати оцінки параметрів моделі, які будуть задовільняти нас.

Отже рівняння моделі набуває вигляду: \[ \hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i \tag{3.4} \] або для нашого прикладу \[ \hat{Weight_i} = \hat{\beta_0} + \hat{\beta_1}Height_i \tag{3.5} \] Давайте для початку проведемо пряму, яка відповідає середньому значенню ваги чоловіків по вибірці:

male %>% 
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  geom_hline(aes(yintercept = mean(Weight_cm)), color = "blue") +
  labs(x = "Зріст (см)",
       y = "Вага (кг)")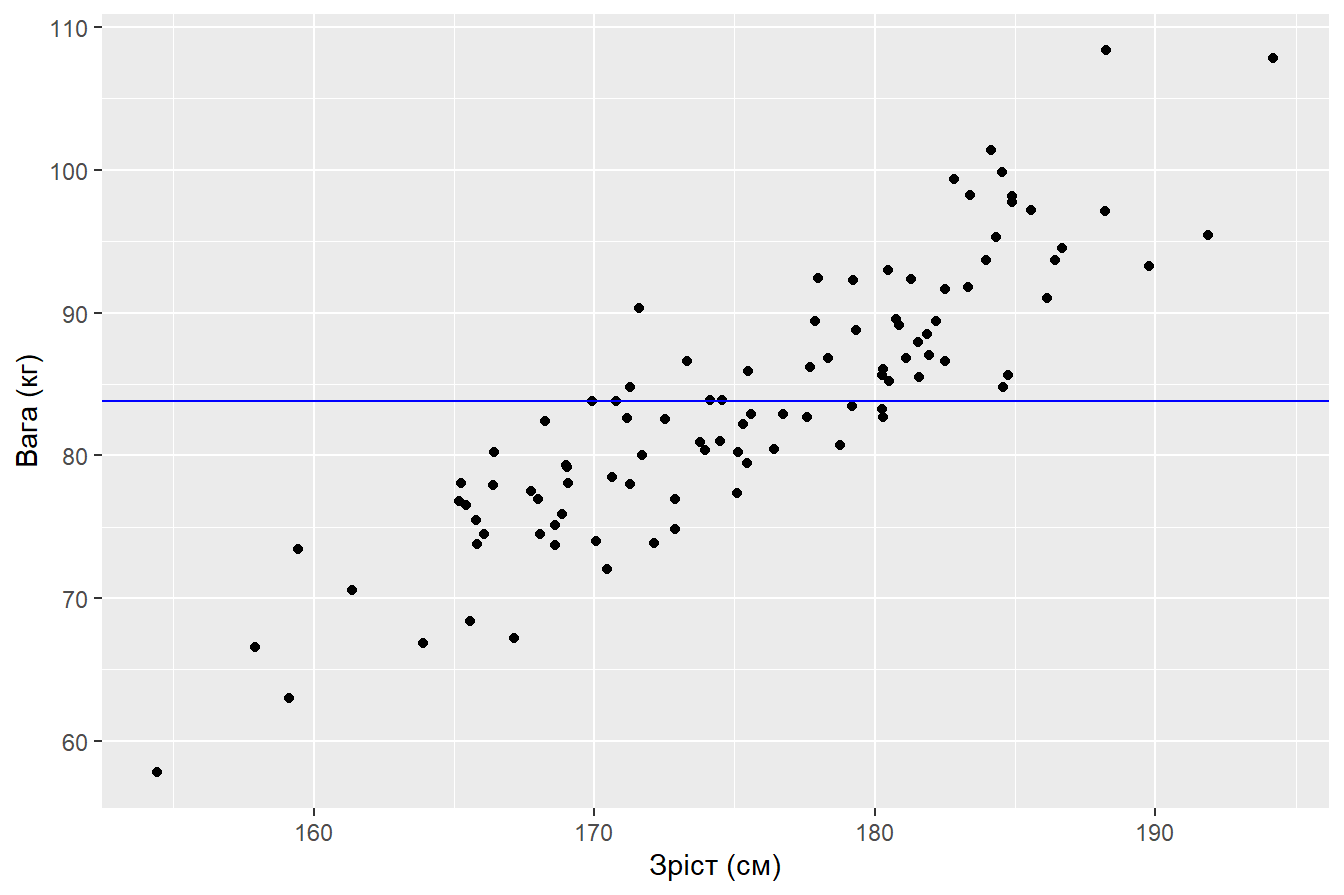

Очевидно, що така “модель” є неоптимальною і вона має значні залишки: відхилення модельних значень від фактичних

male %>% 
  mutate(fit1 = mean(Weight_cm),
         resid1 = Weight_cm - fit1) %>% 
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  geom_hline(aes(yintercept = mean(Weight_cm)), color = "blue") +
  geom_segment(aes(xend = Height_kg, yend = fit1), alpha = 0.2, color = "red") + 
  labs(x = "Зріст (см)",
       y = "Вага (кг)")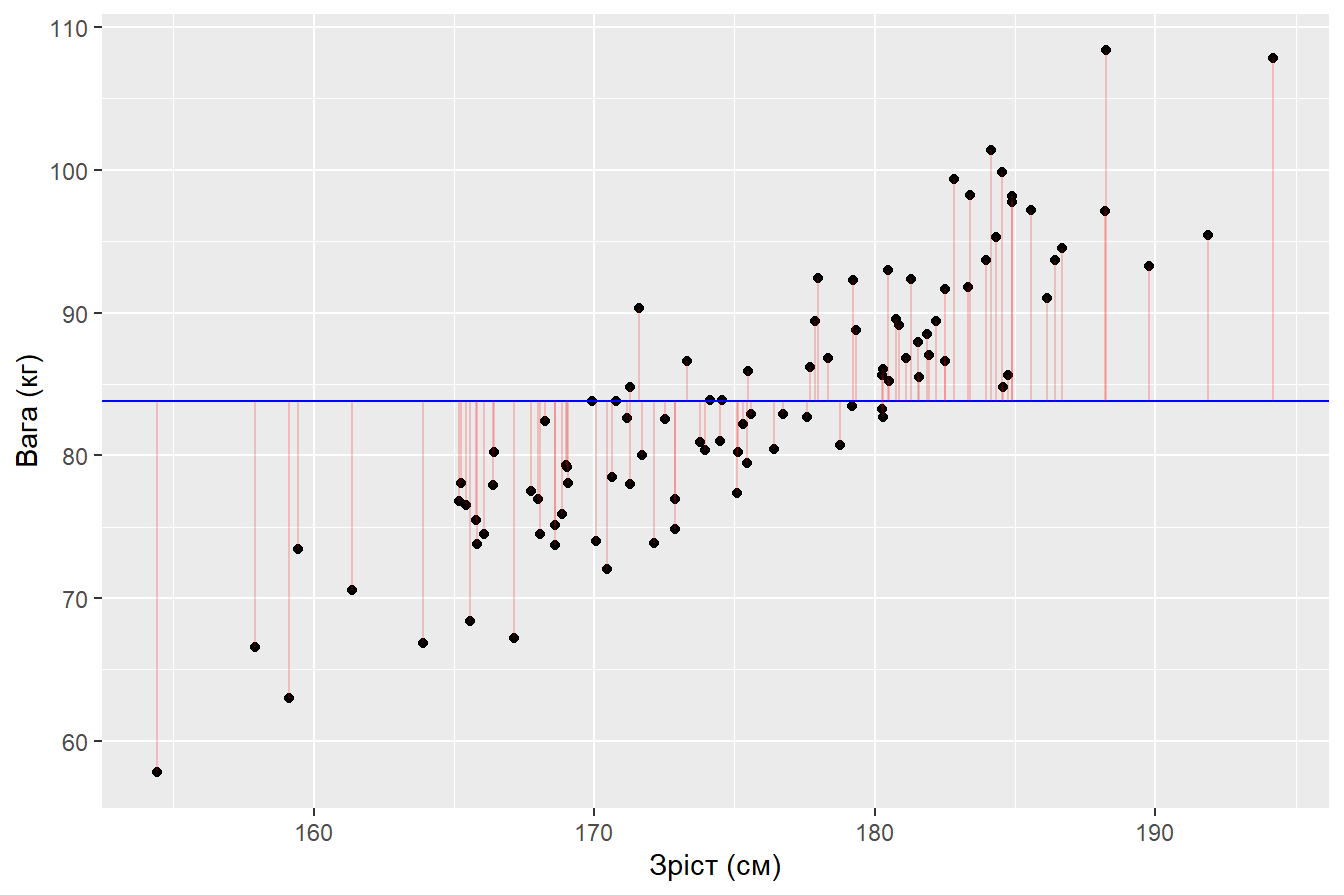

Позитивні відхилення розташовані вище модельних значень, а від’ємні - нижче.

Давайте побудуємо декілька альтернативних прямих

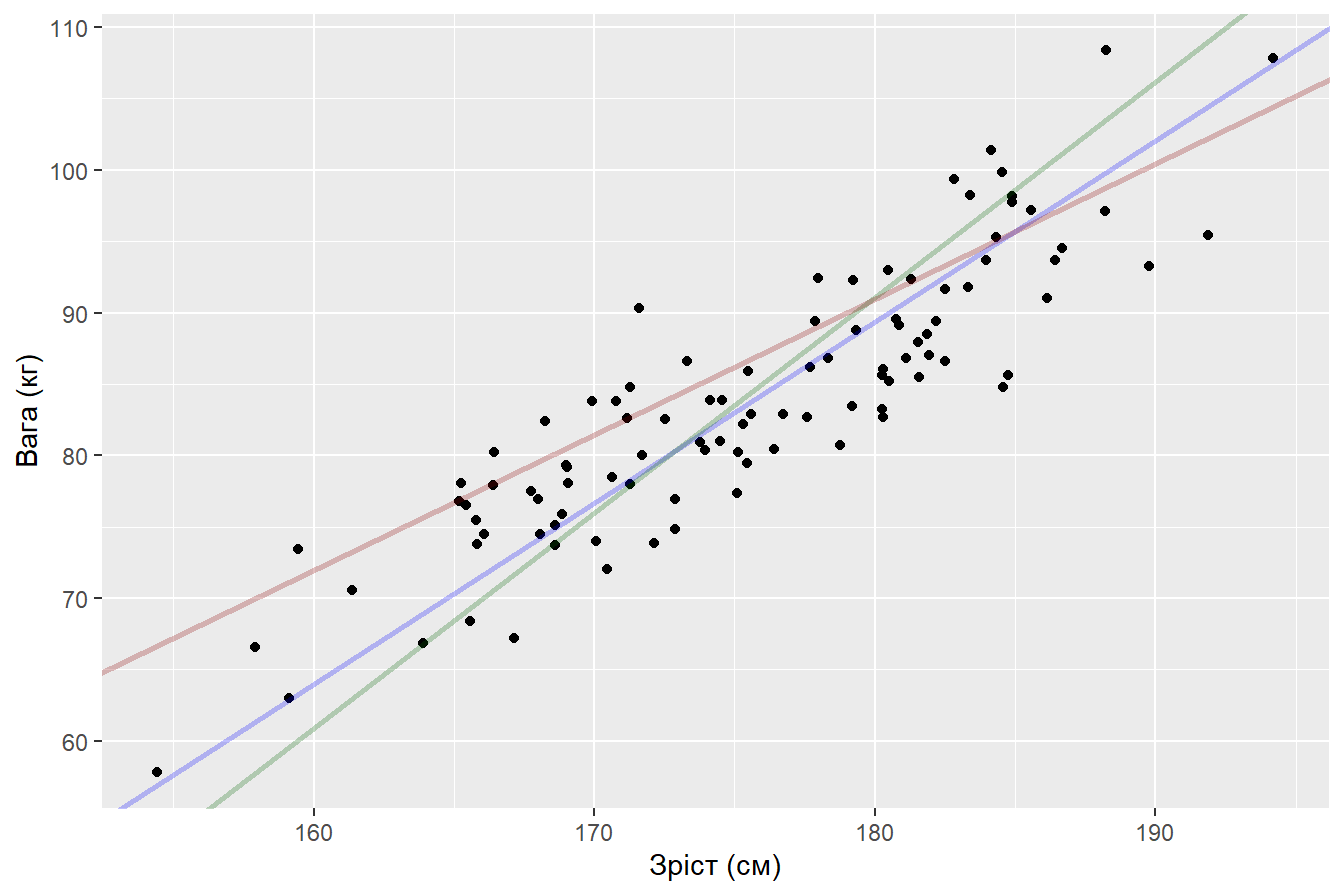
Такі моделі вже мають значно менші відхилення. Але вони були побудовані “на око” без точних математичних розрахунків. Як провести оптимізацію процесу підбору моделі? Для цього ми вводимо функцію втрат (loss function), мінімізуючи котру ми будемо підбирати оптимальні значення \(\hat{\beta_0}\) та \(\hat{\beta_1}\). На перший погляд здається, що непоганою ідеєю було б розрахувати суму похибок \(\sum\limits^{n}_{i=1}{u_i}\) для всіх альтернатив та обрати модель з найменшим значенням. Але такий підхід має значний недолік: представимо, що ми побудували дві моделі і отримали залишки \(u_{m1} = (-10, -5, 5, 10)\) для першої та \(u_{m2} = (-100, -50, 50, 100)\) для другої моделі. Сума залишків для обох моделей дорівнює нулю, але це не значит, що моделі не помиляються. Позитивні та негативні похибки компенсують один одного, при цьому коливання похибок другої моделі значно більші. Тож такий підхід нам не підходить.

Тому для оцінювання параметрів моделі в лінійній регресії пропонується використовувати метод найменших квадратів (МНК, ordinary least squares, OLS): серед альтернатив обbраємо ту, для котрої сума квадратів відхилення буде мінімальною. \[ \sum\limits^{n}_{i=1}{u_i^2} = u_1^2 + u_2^2 + \dots + u_n^2 \rightarrow min \tag{3.6} \] Чому слід брати квадрат відхилення, а не абсолютні значення \(\left |{u_1}\right | + \left |{u_2}\right | + \dots + \left |{u_n}\right |\)? Такий підхід має значний недолік: абсолютні значення не мають неперервної похідної, що робить таку функцію негладкою. До того ж квадрат похибок “штрафують” модель сильніше з більших відхилень. Як альтернативу можна обрати інші парні степені похибок, такі як 4 або 6, але і там є певні складнощі. Тому на практиці частіше за всі інші альтернативи обирають МНК.

Подивимось, як працює мінімізація суми квадратів залишків. \[ \sum\limits^{n}_{i=1}{u_i^2} = \sum\limits^{n}_{i=1}(y_i - \hat{\beta_0} - \hat{\beta_1}x_i)^2 \rightarrow min \tag{3.7} \] Візьмемо похідні по \(\hat{\beta_0}\) та \(\hat{\beta_1}\): \[ \left\{\begin{matrix} -2\sum\limits^{n}_{i=1}(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0 & \\ -2\sum\limits^{n}_{i=1}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0 & \end{matrix}\right. \tag{3.8} \]

Розкриємо дужки першого рівняння: \[ \left\{\begin{matrix} \sum\limits^{n}_{i=1}y_i - n\hat{\beta_0} - \hat{\beta_1}x_i = 0 & \\ \sum\limits^{n}_{i=1}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0 & \end{matrix}\right. \tag{3.9} \]

Поділимо перше рівняння на \(n\): \[ \left\{\begin{matrix} \overline{y} - \hat{\beta_0} - \hat{\beta_1}\overline{x} = 0 & \\ \sum\limits^{n}_{i=1}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0 & \end{matrix}\right. \tag{3.10} \] З першого рівняння виразимо \(\hat{\beta_0}\) і підставимо у друге: \[ \left\{\begin{matrix} \hat{\beta_0} = \overline{y} - \hat{\beta_1}\overline{x} & \\ \sum\limits^{n}_{i=1}x_i(y_i - (\overline{y} - \hat{\beta_1}\overline{x}) - \hat{\beta_1}x_i) = 0 & \end{matrix}\right. \tag{3.11} \] Розкриємо дужки у другому рівнянні: \[ \left\{\begin{matrix} \hat{\beta_0} = \overline{y} - \hat{\beta_1}\overline{x} & \\ \sum\limits^{n}_{i=1}x_i(y_i - \overline{y}) = \hat{\beta_1}\sum\limits^{n}_{i=1}x_i(x_i - \overline{x}) \end{matrix}\right. \tag{3.12} \] Оскільки \[\sum\limits^{n}_{i=1}x_i(y_i - \overline{y}) = \sum\limits^{n}_{i=1}(x_i - \overline{x})^2\] та \[\sum\limits^{n}_{i=1}x_i(y_i - \overline{y}) = \sum\limits^{n}_{i=1}(x_i - \overline{x})(y_i - \overline{y}),\] тоді за умови \[ \sum\limits^{n}_{i=1}(x_i - \overline{x})^2 > 0 \tag{3.13} \] оцінки параметрів моделі \(\hat{\beta_0}\) та \(\hat{\beta_1}\) будуть дорівнювати: \[ \left\{\begin{matrix} \hat{\beta_0} = \overline{y} - \hat{\beta_1}\overline{x} & \\ \hat{\beta_1} = \frac{\sum\limits^{n}_{i=1}(x_i - \overline{x})(y_i - \overline{y})}{\sum\limits^{n}_{i=1}(x_i - \overline{x})^2} = \frac{\overline{xy} - \overline{x}\overline{y}}{\overline{x^2} - \overline{x}^2} \end{matrix}\right. \tag{3.14} \] Давайте поетапно розрахуємо значення \(\hat{\beta_0}\) та \(\hat{\beta_1}\) для нашого прикладу з вагою і зростом:

male %>% 
  select(Height_kg, Weight_cm)
## # A tibble: 100 x 2
##    Height_kg Weight_cm
##        <dbl>     <dbl>
##  1      182.      89.4
##  2      174.      80.9
##  3      175.      83.9
##  4      182.      86.6
##  5      177.      82.9
##  6      184.     101. 
##  7      185.      84.8
##  8      169.      79.2
##  9      170.      74.0
## 10      187.      94.5
## # ... with 90 more rows

Додамо розрахункові значення \(Height_{kg}^2\) та \(Height_{kg}*Weight_{cm}\):

male %>% 
  select(Height_kg, Weight_cm) %>% 
  mutate(Height_kg_sq = Height_kg ^ 2,
         Height_Weight = Height_kg * Weight_cm)
## # A tibble: 100 x 4
##    Height_kg Weight_cm Height_kg_sq Height_Weight
##        <dbl>     <dbl>        <dbl>         <dbl>
##  1      182.      89.4       33197.        16286.
##  2      174.      80.9       30197.        14062.
##  3      175.      83.9       30469.        14644.
##  4      182.      86.6       33302.        15799.
##  5      177.      82.9       31233.        14651.
##  6      184.     101.        33907.        18675.
##  7      185.      84.8       34065.        15647.
##  8      169.      79.2       28566.        13385.
##  9      170.      74.0       28917.        12583.
## 10      187.      94.5       34841.        17637.
## # ... with 90 more rows

Знайдемо середнє значення для кожного стовпчика:

male %>% 
  select(Height_kg, Weight_cm) %>% 
  mutate(Height_kg_sq = Height_kg ^ 2,
         Height_Weight = Height_kg * Weight_cm) %>% 
  summarise(across(Height_kg:Height_Weight,
            mean,
            .names = "mean_{.col}"))
## # A tibble: 1 x 4
##   mean_Height_kg mean_Weight_cm mean_Height_kg_sq mean_Height_Weight
##            <dbl>          <dbl>             <dbl>              <dbl>
## 1           176.           83.8            30892.             14780.

Тепер можемо розрахувати оцінки параметрів моделі:

male %>% 
  select(Height_kg, Weight_cm) %>% 
  mutate(Height_kg_sq = Height_kg ^ 2,
         Height_Weight = Height_kg * Weight_cm) %>% 
  summarise(across(Height_kg:Height_Weight,
            mean,
            .names = "mean_{.col}")) %>% 
  transmute(beta_1 = (mean_Height_Weight - mean_Height_kg * mean_Weight_cm)/(mean_Height_kg_sq - mean_Height_kg^2),
            beta_0 = mean_Weight_cm - beta_1 * mean_Height_kg)
## # A tibble: 1 x 2
##   beta_1 beta_0
##    <dbl>  <dbl>
## 1   1.02  -96.0

Отже рівняння простої лінійної регресії для нашого прикладу буде виглядати: \[\hat{y_i} = -96 + 1.02 * \hat{x}\] Звичайно, на практиці оцінки параметрів моделі за МНК розраховуються за допомогою комп’ютера. Для цього, в R є функція lm(), де першим аргументом вказується формула залежності, а другим набір даних:

# у формулі ліворуч від ~ знаходиться залежна змінна
# праворуч від ~ незалежні змінні
male_ols <- lm(Weight_cm ~ Height_kg, data = male)
male_ols
## 
## Call:
## lm(formula = Weight_cm ~ Height_kg, data = male)
## 
## Coefficients:
## (Intercept)    Height_kg  
##     -95.999        1.024

Результат моделі male_ols зберігається у вигляді списку, з якого ми можемо отримати залишки, параметри моделі, модельні значення тощо:

# Оцінки параметрів моделі
male_ols$coefficients
## (Intercept)   Height_kg 
##  -95.998717    1.024054
# Модельні значення в тібблі
as_tibble(male_ols$fitted.values)
## # A tibble: 100 x 1
##    value
##    <dbl>
##  1  90.6
##  2  82.0
##  3  82.8
##  4  90.9
##  5  85.0
##  6  92.6
##  7  93.0
##  8  77.1
##  9  78.1
## 10  95.1
## # ... with 90 more rows

Побудуємо візуалізацію отриманих результатів за допомогою ggplot2

male %>% 
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(x = "Зріст (см)",
       y = "Вага (кг)")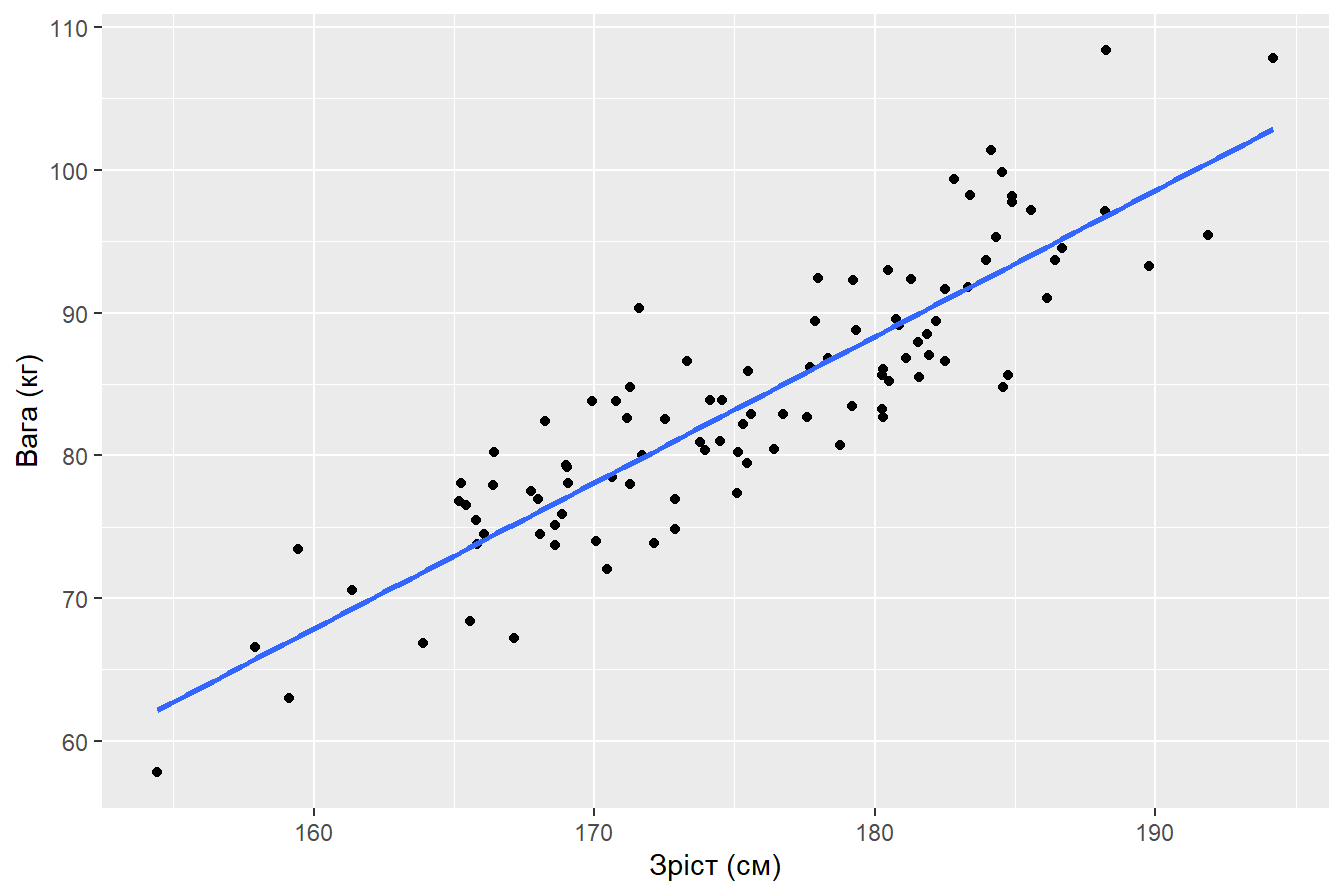

або

male %>% 
  mutate(fit_ols = male_ols$fitted.values) %>% 
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  geom_line(aes(Height_kg, fit_ols), color = "blue") +
  labs(x = "Зріст (см)",
       y = "Вага (кг)")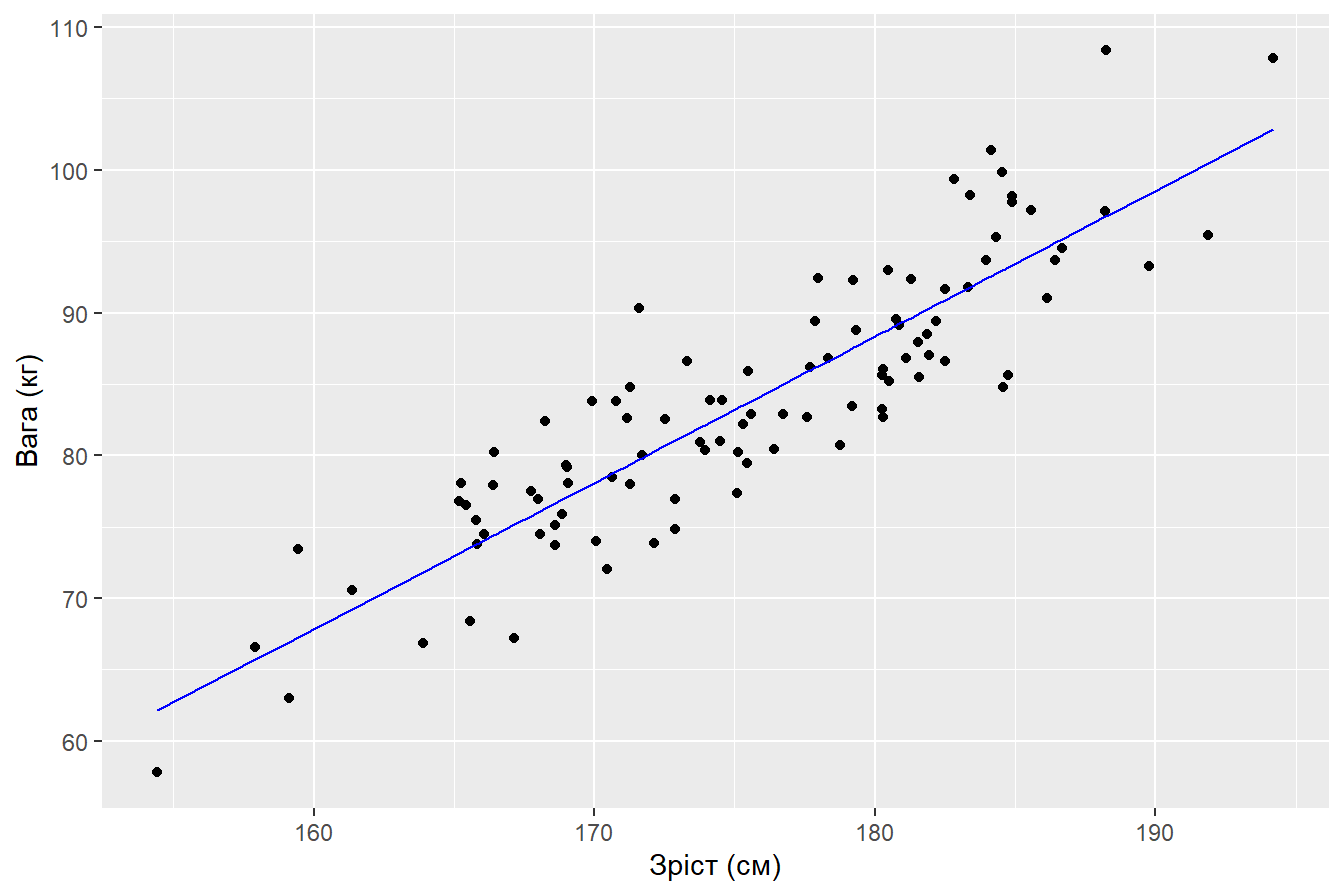

3.2 Властивості модельних значень та залишків

Залишки регресії, які отримані за допомогою МНК мають декілька властивостей:

1. Сума залишків моделі дорівнює нулю: \[ \sum\limits^{n}_{i=1}u_i = 0 \tag{3.15} \]

2. Вибіркова коваріація між регресорами та залишками МНК дорівнює нулю: \[ \sum\limits^{n}_{i=1}x_iu_i = 0 \tag{3.16} \]

3. Лінія регресії завжди проходить через точку \((\overline{x},\overline{y})\)

4. Сума значень залежної змінної дорівнює сумі модельних значень, а отже і їх середні однакові. \[ \sum\limits^{n}_{i=1}y_i = \sum\limits^{n}_{i=1}\hat{y_i} \tag{3.17} \] Ці властивості притаманні кожній моделі, яка побудована з використанням МНК.

Важливо вивести наступні поняття:

• загальна сума квадратів (TSS, total sum of squares): оцінює дисперсію серед \(y_i\), тобто на скільки дані розсіяні у вибірці. Якщо поділити SST на \(n-1\), ми отримаємо вибіркову дисперсію значень \(y_i\). \[ TSS = \sum\limits^{n}_{i=1}(y_i - \overline{y})^2, \tag{3.18} \]

• пояснювальна сума квадратів (ESS, explained/estimated sum of squares): оцінює міру розсіювання \(\hat{y_i}\) (3.17). \[ ESS = \sum\limits^{n}_{i=1}(\hat{y_i} - \overline{y})^2, \tag{3.19} \]

• сума квадратів залишків (RSS, residual sum of squares): оцінює розсіювання серед \(\hat{u_i}\). \[ RSS = \sum\limits^{n}_{i=1}{u_i^2} \tag{3.20} \] TSS може визначена через суму SSE та SSR: \[ TSS = ESS + RSS \tag{3.21} \] Окремо зверну увагу на абрівіатури цих показників в різних джерелах:

• TSS іноді записують, як SST.

• ESS іноді записують, як RSS (regression sum of squares).

• RSS іноді вживають, як SSR (sum of squared residuals) або ESS (error sum of squares).

Будьте уважні!

3.3 Коефіцієнт детермінації

Тепер слід визначити, наскільки пояснювальна змінна \(x_i\) пояснює пояснювальну змінну \(y_i\).

Якщо припустити, що TSS не дорівнює нулю (це можливо тільки в тому випадку коли всі \(y_i\) однакові), ми можемо поділити (3.21) на TSS. В результаті, ми отримаємо коефіцієнт детермінації або \(R^2\) (R-квадрат): \[ R^2 = \frac{ESS}{TSS} = 1 - \frac{RSS}{TSS} = 1 - \frac{\sum\limits^{n}_{i=1}{u_i^2}}{\sum\limits^{n}_{i=1}(y_i - \overline{y})^2} \tag{3.22} \] \(R^2\) показує, яка частина варіації (розсіювання) \(y_i\) пояснюється \(x_i\). Цей показник знаходиться завжди в межах від нуля до одиниці \([0,1]\). Для інтерпретації у відсотках, \(R^2\) домножують на 100: який відсоток варіації \(y_i\) пояснюється \(x_i\). Чим ближчий \(R^2\) до 1 - тим краще \(x_i\) пояснює \(y_i\) і навпаки, чим ближчий \(R^2\) до 0 - тим гіршу модель ми отримали.

Також \(R^2\) можна пояснити, як квадрат коефіцієнта кореляції між \(y_i\) та \(\hat{y_i}\).

Коефіцієнта кореляції (r, correlation coefficien) — показник, який показує силу лінійного взаємозв’язку між двома змінними: \[ r = \frac{n\sum\limits^{n}_{i=1}(xy) - \sum\limits^{n}_{i=1}x_i\sum\limits^{n}_{i=1}y_i}{\sqrt{[n\sum\limits^{n}_{i=1}x^2 - (\sum\limits^{n}_{i=1}x_i)^2][n\sum\limits^{n}_{i=1}y_i^2-(\sum\limits^{n}_{i=1}y_i)^2]}} \tag{3.23} \] \(r\) змінюється від мінус одиниці до одиниці \([-1,1]\):

• при наближенні до -1 присутній обернений взаємозв’язок між змінними (одна зростає, інша спадає і навпаки)

• при наближенні до +1 присутній прямий лінійний взаємозв’язок між змінними (одна зростає й інша зростає і навпаки)

• при наближенні до 0 лінійного взаємозв’язку між змінними не існує.

Для розрахунку коефіцієнта кореляції в R використовується функція cor():

cor(male$Weight_cm, male$Height_kg)
## [1] 0.8862974

Тоді коефіцієнт детермінації має дорівнювати:

cor(male$Weight_cm, male$Height_kg)^2
## [1] 0.7855231

Давайте розрахуємо \(R^2\) вручну (3.22):

1 - sum(male_ols$residuals^2) / sum((male$Weight_cm - mean(male$Weight_cm))^2)
## [1] 0.7855231

Але все теж саме можна отримати застосувавши функцію summary() до МНК моделі:

male_ols %>% 
  summary()
## 
## Call:
## lm(formula = Weight_cm ~ Height_kg, data = male)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.2309 -3.3608  0.0104  3.1405 11.6086 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -95.99872    9.50045  -10.11   <2e-16 ***
## Height_kg     1.02405    0.05405   18.95   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.314 on 98 degrees of freedom
## Multiple R-squared:  0.7855, Adjusted R-squared:  0.7833 
## F-statistic: 358.9 on 1 and 98 DF,  p-value: < 2.2e-16

Функція summary() виводить багато різноманітної інформації щодо побудованої моделі, з кожним елементом якої ми познайомимось вже згодом.

З точки зору інтерпретації результатів по \(R^2\) слід сказати, що 78.5% варіації ваги чоловіків пояснюється їх зростом, а 21.5% пояснюються іншими показниками, які не входять у дослідження.

На практиці можна досить часто зустріти маленькі значення \(R^2\), але це ще не означає, що побудована модель є неефективною. Критеріїв ефективності моделей, як і задач які вони мають вирішувати досить багато, тому не слід концентруватися виключно на коефіцієнті детермінації.

3.4 Передумови використання МНК

Нагадаю, що є принципова відмінність між параметрами моделі \(\beta_j\) та \(\hat{\beta_j}\):

• \(\beta_j\) (без “кришки”) — це істинні параметри моделі, котрі на практиці ніколи не відомі, тому що ми не маємо у розпорядженні генеральну сукупність даних щодо об’єкту дослідження. Якщо повернутися до прикладу зі зростом та вагою серед чоловіків, тоді нам потрібно було б зібрати цю інформацію для всієї чоловічої половини населення планети, але це неможливо.

• \(\hat{\beta_j}\) (з “кришкою”) — це наближені оцінки параметрів моделі, які були отримані за допомогою вибірки даних. Як правило, така вибірка є випадковою, а отже і оцінки параметрів моделі є випадковими величинами.

І тут постає питання: за яких умов ми можемо довіряти оцінкам параметрів моделі? Ці умови називають передумовами МНК:

1. Модель лінійна за параметрами і має коректну специфікацію. Якщо дані мають нелінійну природу та/або формула задана некоректно (про це трошки пізніше), очікувати на коректні результати від такої моделі не має сенсу.

2. Випадковість вибірки даних. Якщо б в нашому прикладі з вагою і зростом були зібрана інформація тільки по високим чоловікам, то й узагальнення на основі моделі стосувалися б тільки високих чоловіків, а не всіх чоловіків планети.

3. Неоднаковість та незалежність змінних \(x_i\). Явище кореляції між пояснювальними змінними називається мультиколінеарністю і вона призводить до неефективності параметрів моделі з точки зору їх інтерпретації.

4. Математичне сподівання залишків моделі дорівнює нулю \(E(u_i) = 0\). Це припущення говорить по те, що серед залишків моделі будуть як позитивні, так і негативні значення, але вони компенсують один одного.

5. Гомоскедастичність (постійність) залишків моделі \(Var(u_i) = \sigma^2\). Непостійність залишків призводить до значних проблем в моделі, явище гетероскедастичності (протилежність до гомоскедастичності) ми розглянемо в окремій темі.

6. Незалежність залишків моделі. Якщо залишки корелюють між собою, це означає, що в них залишилась “корисна” інформація, яку наша модель не змогла визначити.

7. Залишки моделі мають нормальний розподіл \(N(0, \sigma^2)\). Ця властивість буде корисною при тестуванні різноманітних гіпотез та побудові довірчих інтервалів.

На практиці, ви досить часто будете зустрічати ситуації коли одна або одразу декілька (якщо не всі) передумов МНК не будуть виконуватись. Звичайно є альтернативні методи та моделі для побудови регресійних задач, але саме проста лінійна регресія є фундаментом, від котрого всі відштовхуються. Це як таблиця множення, розуміння і вміння нею користуватися значно полегшує подальшу роботу.

3.5 Значущість оцінок параметрів моделі

Я вже говорив, що оцінки параметрів моделі \(\hat{\beta_0}\) та \(\hat{\beta_1}\) є випадковими величинами, які “приблизно” оцінюють істині параметри моделі \({\beta_0}\) та \({\beta_1}\). Якщо істинні параметри моделі дорівнюють нулю, скоріш за все їх оцінки будуть дещо відхилятися від нуля і навпаки. Тож нам слід вміти визначати статистичну значущість оцінок параметрів моделі — впевненість в тому, що параметри моделі не дорівнюють нулю.

В якості статистичного критерію використовуються t-критерій Стьюдента: \[ t_{\beta_j} = \frac{\hat{\beta_j}}{se(\hat\beta_j)}, \tag{3.24} \] де \(se(\hat\beta_j)\) — стандартна похибка \(\hat\beta_j)\), для розрахунку котрої необхідно визначити дисперсію \(\hat\beta_j)\).

Я залишу поза межами цього підручника доведення відповідних теорем, але якщо комусь буде цікаво ознайомитись, пропоную почитати роботи (Wooldridge 2019; Kleiber 2006).

Дисперсія оцінки параметру моделі \(\hat{\beta_1}\) дорівнює: \[ \hat{var}(\hat{\beta_1}) = \frac{S^2}{\sum\limits^{n}_{i=1}(x_i - \overline{x})^2}, \tag{3.25} \] де \[ S^2 = \frac{1}{n-2}\sum\limits^{n}_{i=1}u_i^2 \tag{3.26} \] Корінь квадратний з (3.26) називається стандартною помилкою оцінки параметру \(\hat{\beta_1}\): \[ se(\hat{\beta_1}) = \sqrt{\hat{var}(\hat{\beta_1})} = \sqrt{\frac{S^2}{\sum\limits^{n}_{i=1}(x_i - \overline{x})^2}} \tag{3.27} \]

Аналогічним чином розраховується стандартна помилка оцінки параметру \(\hat{\beta_0}\): \[ se(\hat{\beta_0}) = \sqrt{\hat{var}(\hat{\beta_0})} = \sqrt{\frac{\frac{S^2}{n}\sum\limits^{n}_{i=1}x_i^2}{\sum\limits^{n}_{i=1}(x_i - \overline{x})^2}} \tag{3.28} \] Тепер ми знаємо, як розрахувати критерій Стьюдента (3.24), який перевіряє значущість \(\hat{\beta_j}\) за наступною процедурою:

1. Формуємо дві гіпотези:

• \(H_0:{\beta_j}=0\): параметр незначущій.
• \(H_1:{\beta_j}\neq 0\): параметр значущій.

2. Розраховуємо критерій Стьюдента (3.24).

3. Обираємо рівень значущості \(\alpha\) — це ймовірність помилки першого роду, тобто ймовірність відхилити гіпотезу за умови, що вона правильна. На практиці \(\alpha\) беруть 5% (0.05), хоча все залежить від сфери дослідження.

4. Знаходимо критичне значення критерія Стьюдента \(t_{df}^{\alpha/2}\) для заданого рівня значущості \(\alpha\) та ступеня свободи \(df\). Для цього використовується таблиця розподілу Стьюдента або функція в R qt().

5. Порівнюємо абсолютне значення \(t_{\beta_j}\) з \(t_{df}^{\alpha/2}\):

• якщо \(|t_{\beta_j}| > t_{df}^{\alpha/2}\) — відхиляємо нульову гіпотезу. Це означає, що \(\beta_j\) є статистично значущою і не дорівнює нулю.
• якщо \(|t_{\beta_j}| < t_{df}^{\alpha/2}\) — нульова гіпотеза не може бути відхилена. Тобто \(\beta_j\) є статистично незначущою.

Альтернативна процедура до оцінювання статистичної значущості параметрів моделі є p-значення (читається пі-значення, p-value) — такий рівень значущості, за котрого гіпотеза знаходиться на межі між відхиленням і прийняттям.

Використовувати його дуже легко:

• якщо p-значення менше обраного рівня значущості \(\alpha\) — відхиляємо нульову гіпотезу.

• якщо p-значення більше обраного рівня значущості \(\alpha\) — нульова гіпотеза не може бути відхилена.

3.6 Довірчі інтервали оцінок параметрів моделі

Довірчий інтервал (ДІ, confidence interval, CI) — діапазон значень в який потрапляє випадкова величина з певною ймовірністю.

Довірчий інтервал для оцінок параметрів моделі розраховується за формулою: \[ \hat{\beta_j} - se(\hat{\beta_j}) \times t_{df}^{\alpha/2} < \beta_j < \hat{\beta_j} + se(\hat{\beta_j}) \times t_{df}^{\alpha/2} \tag{3.29} \]

Тобто з йомовірністю \(1 - \alpha\) інтервал \((\hat{\beta_j} - se(\hat{\beta_j})*t_{df}^{\alpha/2}, \hat{\beta_j} + se(\hat{\beta_j})*t_{df}^{\alpha/2})\) буде містити істинні значення параметру моделі.

Розрахуємо довірчі інтервали до оцінок параметрів моделі з нашого прикладу. В R для цього використовується функція confint():

confint(male_ols)
##                    2.5 %     97.5 %
## (Intercept) -114.8520605 -77.145374
## Height_kg      0.9167876   1.131321

Довірчі інтервали більш інформативні ніж просто точкові оцінки. Погодьтесь, що твердження “параметр \(\hat\beta_1\) дорівнює 1.02405 менш інформативно, ніж”з ймовірністю 95% істинне значення параметру моделі \(\hat\beta_1\) знаходиться в межах від 0.9167896 до 1.13131. Крім того, якщо довірчий інтервал перетинає нуль - це вказує на його статистичну незначущість.

3.7 Розрахунок статистик в R

Повернемось до нашого прикладу з вагою і зростом.

Всі зазначені показники (крім довірчих інтервалів) розраховуються за допомогою функції summary() застосованої до побудованої моделі:

male_ols %>% 
  summary()

1. У розділі Residuals наведено розподіл залишків моделі:

Residuals:
    Min      1Q  Median      3Q     Max 
-8.2309 -3.3608  0.0104  3.1405 11.6086 

• мінімальне значення (Min): -8.2309

• перший квартиль (1Q): -3.3608

• медіана (Median): 0.0104

• третій квартиль (3Q): 3.1405

• максимальне значення (Max): 11.6086

За бажання можна візуалізувати розподіл залишків моделі:

male_ols$residuals %>% 
  as_tibble() %>% 
  ggplot(aes(x = "male", y = value)) + 
  geom_boxplot(width = 0.6) +
  stat_summary(
    aes(label=sprintf("%1.1f", ..y..)),
    geom = "text", 
    fun = function(y) boxplot.stats(y)$stats,
    position = position_nudge(x = 0.33))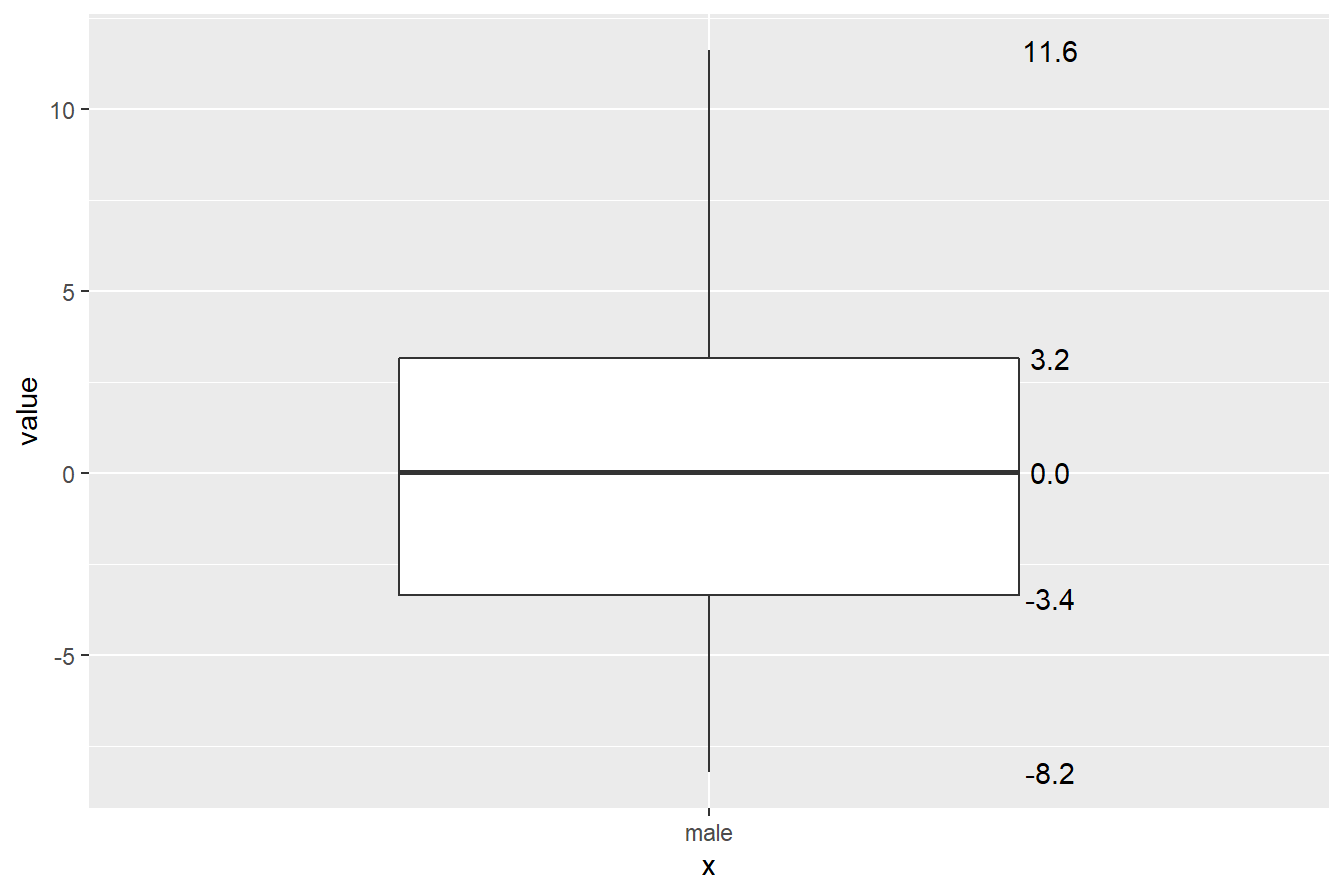

2. У розділі Coefficients відображається таблиця про оцінки параметрів моделі:

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -95.99872    9.50045  -10.11   <2e-16 ***
Height_kg     1.02405    0.05405   18.95   <2e-16 ***

• Estimate: значення оцінок параметрів

• Std. Error: стандартні похибки оцінок параметрів

• t value: значення критерію Стюдента

• Pr(>|t|): p-значення. Зірочки вказують на значущість параметрів моделі, що спрощує візуальне сприйняття результатів.

Розшифровку зірочок ви можете бачити у розділі Signif. codes:

Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

• ‘***‘ - p-значення наближається до нуля.

• ‘**‘ - p-значення близько 0.001

• ‘*‘ - p-значення близько 0.05

• ‘.‘ - p-значення близько 0.1

• ‘ ‘ - p-значення більше 0.1

Останні три рядка ми розберемо згодом.

3.8 Точковий та інтервальний прогноз

Крім пояснення сили впливу незалежної змінної на залежну, лінійна регресія дає можливість будувати прогнози. У випадку перехресних даних ми відповідаємо на питання “що-якщо?” тобто визначаємо значення \(y_{n+1}\) за заданого значення \(x_{n+1}\). У випадку часових рядів - визначаємо, чому буде дорівнювати залежна змінна в наступні періоди часу.

Формула для розрахунку точкового прогнозу: \[ \hat{y}_{n+1} = \hat{\beta_0} + \hat{\beta_1}x_{n+1} \tag{3.30} \] Але й тут необхідно розраховувати довірчі інтервали до прогнозних значень. Для цього нам необхідно знати стандартну похибку пронозу: \[ \delta = \sqrt{S^2 (1 + \frac{1}{n} + \frac{(x_{n+1} - \overline{x})^2}{\sum\limits^{n}_{i=1}(x_i - \overline{x})^2})} \tag{3.31} \] Тоді прогнозний інтервал: \[ \hat{y}_{n+1} - \delta*t_{df}^{\alpha/2} < {y}_{n+1} < \hat{y}_{n+1} + \delta*t_{df}^{\alpha/2} \tag{3.32} \]

Для побудови прогнозу в R використовується функція predict(), де необхідно вказати модель та нові значення для прогнозу.

В якості прикладу створимо новий датасет з тьома новими значеннями зросту для чоловіків: 186 см, 192 см та 200 см. І передамо ці значення у функцію predict(). В результаті для кожного нового значення отримуємо точкові прогнози:

new_height <- tibble(Height_kg = c(186, 192, 200))
predict(male_ols, newdata = new_height)
##         1         2         3 
##  94.47537 100.61970 108.81213

Для отримання прогнозів з довірчими інтервалами, необіхдно додатки аргумент interval = "prediction" до функції predict(). З замовчуванням будується 95% довірчий інтервал, де lwr та upr — верхня та нижня межа довірчих інтервалів.

predict(male_ols, newdata = new_height, interval = "prediction")
##         fit      lwr      upr
## 1  94.47537 85.80017 103.1506
## 2 100.61970 91.83835 109.4010
## 3 108.81213 99.81929 117.8050

Для інтерпретації результатів можна сказати, що згідно нашої моделі, 95% чоловіків зі зростом 200 сантиметрів мають вагу від 99.81929 до 117.8050 кілограмів.

Як альтернативу, можна використати аргумент interval = "confidence" для побудови довірчого інтервалу до середнього прогнозу:

predict(male_ols, newdata = new_height, interval = "confidence")
##         fit       lwr       upr
## 1  94.47537  93.06753  95.88321
## 2 100.61970  98.66140 102.57800
## 3 108.81213 106.05638 111.56789

В такому випадку інтерпретація буде наступна: згідно нашої моделі, чоловічки зі зростом 200 сантиметрів мають в середньому вагу від 106.05638 до 111.56789 кілограмів.

Що обрати, довірчий інтервал до середнього прогнозу чи інтервальний прогноз? Інтервальний прогнозу оцінює невизначеність щодо конкретного значення, а довірчий інтервал щодо середнього значення. Це означає, що інтервальний прогноз буде значно ширший за довірчий інтервал. Тож вибір залежить від цілей та контексту аналізу. Частіше нас цікавлять конкретні індивідуальні значення прогнозів, тож інтервальні прогнози використовуються частіше (Bruce and Bruce 2017).

Наступний код демонструє різницю між довірчим інтервалом (сірий) та інтервальним прогнозом (червоний):

# 1. Будуємо прогнозні значення за моделью за реальними даними
pred.int <- predict(male_ols, interval = "prediction")

male %>% 
  # 2. Об'єднуємо стовпчики
  bind_cols(pred.int) %>% 
  # 3. Будуємо графік
  ggplot(aes(Height_kg, Weight_cm)) +
  geom_point() +
  # 4. Додаємо лінію регресії та довірчий інтервал
  geom_smooth(method = "lm") +
  # 5. Додаємо інтервальні прогнози
  geom_line(aes(y = lwr), color = "red", linetype = "dashed") +
  geom_line(aes(y = upr), color = "red", linetype = "dashed") +
  labs(x = "Зріст (см)",
       y = "Вага (кг)")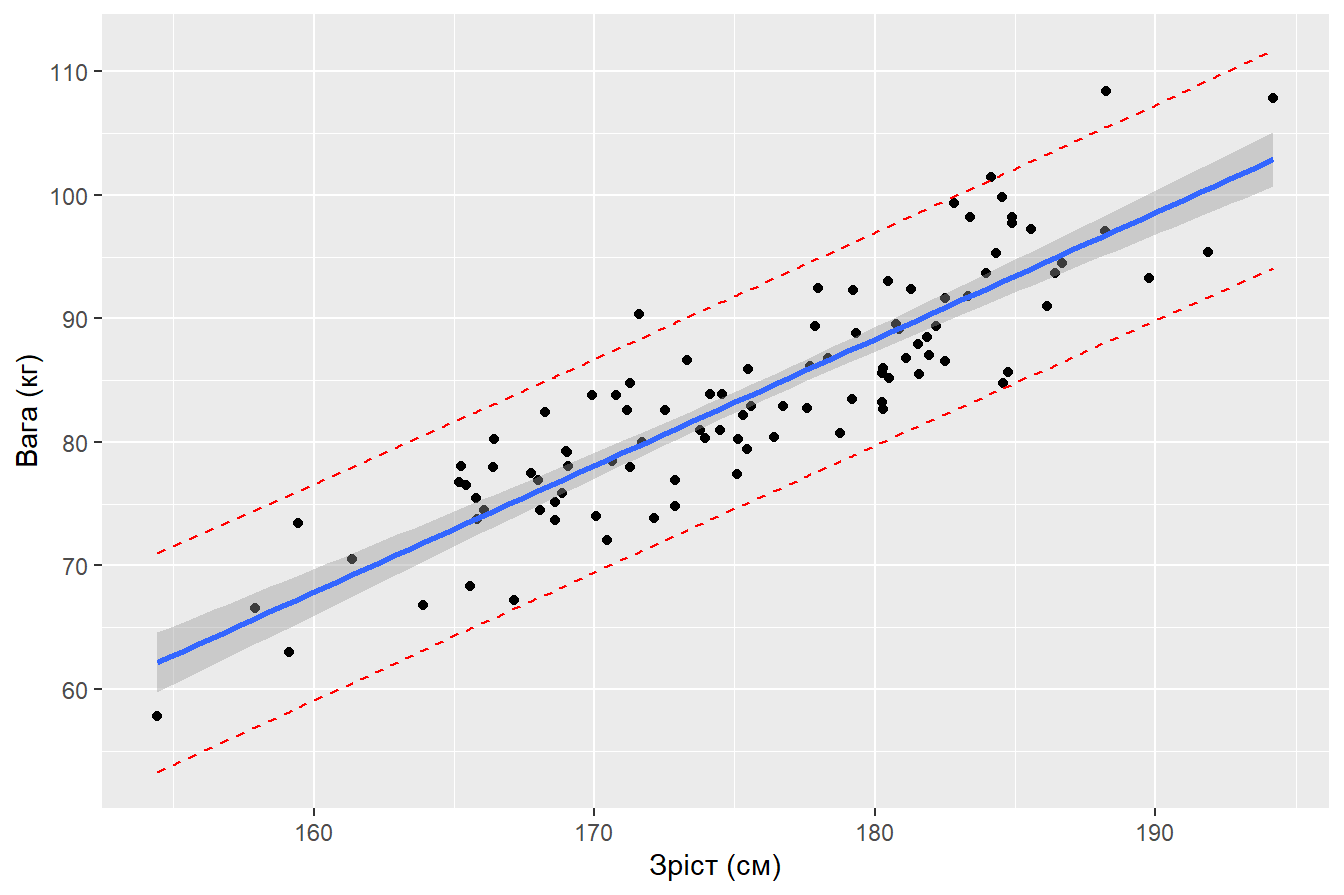

3.9 Завдання

3.9.1 Обрати та завантажити дані

Для практичних та лабораторних робіт необхідно знайти та обрати дані з якими бажаєте працювати. Для цього рекомендую наступні джерела:

• Сервіс з пошуку даних від Google Dataset Search

• Репозитарій з машинного навчання UCI

• Дані Всісвітнього банку

• Набори даних з біостатистики

• Платформа змагать Kaggle

• Fuel Economy Data

Вимоги до датасетів прості: мають бути цікавими для Вас та наявність числових змінних (більше двох). Можете пошукати щось додатково в гуглі.

Завантажте дані в R.

3.9.2 Обробка даних

Після завантаження даних, за потреби приведіть їх до охайного вигляду, створіть нові змінні або перекодуйте вже існуючі.

3.9.3 Лінійна регресія

Всі завдання виконуються у двох напрямках: вручну (всі розрахунки будуєте самостійно) та за допомогою функцій мови програмування R.

1. Оберіть дві числові змінні з завантаженого набору даних. Визначте, яка змінна буде залежною, а яка незалежною.

2. Побудуйте точкову діаграму. Як ви можете описати отриманий результат?

3. Розрахуйте коефіцієнт кореляції. Зробіть висновки.

4. Побудуйте модель простої лінійної регресії за допомогою формул та за допомогою функції lm(). Порівняйте результати. Запишіть рівняння регресії.

5. Відобразіть на графіку точкової діаграми лінію регресії.

6. Розрахуйте стандартні похибки оцінок параметрів моделі.

7. Розрахуйте t-критерій Стьюдента до оцінок параметрів моделі. Порівняйте з табличним значенням або розрахуйте p-значення. Зробіть висновки щодо гіпотез.

8. Побудуйте довірчі інтервали до оцінок параметрів моделі.

9. Розрахуйте коефіцієнт детермінації. Зробіть висновок щодо його значення.

10. Побудуйте точковий та інтервальний прогноз за побудованою моделью за довільними значеннями незалежної змінної.